Молекулярно-кінетична теорія дозволяє, аналізуючи мікроскопічне поведінку системи і використовуючи методи статистичної механіки, отримати важливі макроскопічні характеристики термодинамічної системи. Однією з мікроскопічних характеристик, яка пов’язана з температурою системи, є середня квадратична швидкість молекул газу. Формулу для неї наведемо й розглянемо у статті.
Ідеальний Газ
Відразу зазначимо, що формула середньої квадратичної швидкості молекул газу буде приведена саме для ідеального газу. Під ним у фізиці вважають таку многочастичную систему, в якій частинки (атоми, молекули) не взаємодіють один з одним (їх кінетична енергія на кілька порядків перевищує потенційну енергію взаємодії) і не мають розмірів, тобто є точками з кінцевою масою (відстань між частинками на кілька порядків перевищує їх лінійні розміри).
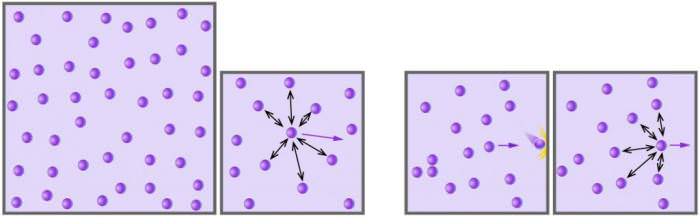
Будь газ, який складається з хімічно нейтральних молекул або атомів, і що знаходиться під невеликим тиском і має високу температуру, може вважатися ідеальним. Наприклад, повітря – це ідеальний газ, а водяна пара таким вже не є (між молекулами води діють сильні водневі зв’язки).