У природі і техніці ми часто стикаємося з проявом обертального руху твердих тіл, наприклад, валів і шестерень. Як у фізиці описують цей тип руху, які формули і рівняння для цього застосовуються, ці та інші питання висвітлюються в даній статті.
Що таке обертання?
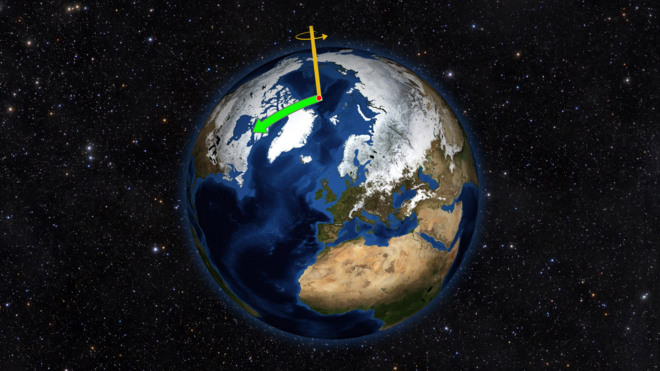
Кожен з нас інтуїтивно уявляє, про який рух піде мова. Обертання – це процес, при якому тіло та матеріальна точка рухається по круговій траєкторії навколо деякої осі. З геометричної точки зору вісь обертання твердого тіла – це пряма, відстань до якої в процесі переміщення залишається незмінним. Цю відстань називають радіусом обертання. Далі будемо позначати його буквою r. Якщо вісь обертання проходить через центр мас тіла, то її називають власною віссю. Прикладом обертання навколо власної осі є відповідний рух планет Сонячної системи.
Щоб обертання відбувалося, має існувати центростремительное прискорення, яке виникає за рахунок доцентрової сили. Ця сила спрямована від центру мас тіла до осі обертання. Природа доцентрової сили може бути самою різною. Так, в космічному масштабі її роль виконує гравітація, якщо тіло закріплено ниткою, то сила натягу останньої буде доцентрової. Коли тіло обертається навколо власної осі, роль доцентрової сили відіграє внутрішнє електрохімічне взаємодія між складовими тіло елементами (молекулами, атомами).
Необхідно розуміти, що без присутності доцентрової сили тіло буде рухатися прямолінійно.
Описують обертання фізичні величини
По-перше, це динамічні характеристики. До них відносяться:
- момент імпульсу L;
- момент інерції I;
- момент сили M.
По-друге, це кінематичні характеристики. Перерахуємо їх:
- кут повороту θ;
- кутова швидкість ω;
- кутове прискорення α.
Коротко опишемо кожну з названих величин.
Момент імпульсу визначається за формулою:
L = p*r = m*v*r
Де p – лінійний імпульс, m – маса матеріальної точки, v – її лінійна швидкість.
Момент інерції матеріальної точки розраховується за допомогою виразу:
I = m*r2
Для будь-якого тіла складної форми величина I розраховується, як інтегральна сума моментів інерції матеріальних точок.
Момент сили M обчислюється так:
M = F*d
Тут F – зовнішня сила, d – відстань від точки її прикладення до осі обертання.
Фізичний сенс всіх величин, в назві яких присутнє слово “момент”, аналогічно змістом відповідних лінійних величин. Наприклад, момент сили показує можливість прикладеної сили повідомити кутове прискорення системі обертаються тел.
Кінематичні характеристики математично визначаються наступними формулами:
ω = dθ/dt;
α = dω/dt.
Як видно з цих виразів, кутові характеристики аналогічні за своїм змістом лінійним (швидкості v і прискорення a), тільки вони застосовні для кругової траєкторії.
Динаміка обертання
У фізиці вивчення обертального руху твердого тіла здійснюється з допомогою двох розділів механіки: динаміки і кінематики. Почнемо з динаміки.
Динаміка вивчає зовнішні сили, діючі на систему обертових тел. Відразу запишемо рівняння обертального руху твердого тіла, а потім, розберемо його складові частини. Отже, це рівняння має вигляд:
M = I*α
Момент сили, що діє на систему, що володіє моментом інерції I, викликає появу кутового прискорення α. Чим менше величина I, тим легше з допомогою певного моменту M розкрутити систему до великих швидкостей за малі проміжки часу. Наприклад, металевий стрижень легше обертати уздовж його осі, ніж перпендикулярно їй. Однак, той же стрижень легше обертати навколо осі, перпендикулярній йому, і проходить через центр мас, ніж через його кінець.
Закон збереження величини L
Вище була введена ця величина, вона називається моментом імпульсу. Рівняння обертального руху твердого тіла, представлене в попередньому пункті, часто записують в іншій формі:
M*dt = dL
Якщо момент зовнішніх сил M діє на систему протягом часу dt, то він викликає зміну моменту імпульсу системи на величину dL. Відповідно, якщо момент сил дорівнює нулю, тоді L = const. Це і є закон збереження величини L. Для неї, використовуючи зв’язок між лінійною і кутовою швидкістю, можна записати:
L = m*v*r = m*ω*r2 = I*ω.
Таким чином, при відсутності моменту сил добуток кутової швидкості та моменту інерції є постійною величиною. Цей фізичний закон використовують фігуристи у своїх виступах або штучні супутники, які необхідно повернути навколо власної осі у відкритому космосі.
Центростремительное прискорення
Вище, при вивченні обертального руху твердого тіла, вже була описана ця величина. Також була відзначена природа доцентрових сил. Тут лише доповнимо цю інформацію і приведемо відповідні формули для розрахунку цього прискорення. Позначимо його ac.
Оскільки доцентрова сила спрямована перпендикулярно осі і проходить через неї, то моменту вона не створює. Тобто ця сила не має абсолютно ніякого впливу на кінематичні характеристики обертання. Тим не менш, вона створює центростремительное прискорення. Наведемо дві формули для його визначення:
ac = v2/r;
ac = ω2*r.
Таким чином, чим більше кутова швидкість і радіус, тим більшу силу треба прикласти, щоб утримати тіло на круговій траєкторії. Яскравим прикладом цього фізичного процесу є занос автомобіля під час повороту. Занос виникає, якщо доцентрова сила, роль якої грає сила тертя, стає менше, ніж відцентрова сила (інерційна характеристика).
Кінематика обертання
Три основні кінематичні характеристики були перераховані вище в статті. Кінематика обертального руху твердого тіла формулами описується наступними:
θ = ω*t => ω = const., α = 0;
θ = ω0*t + α*t2/2 => ω = ω0 + α*t, α = const.
У першій рядку наведено формули для рівномірного обертання, яке передбачає відсутність зовнішнього моменту сил, що діє на систему. У другому рядку записані формули для равноускоренного руху по колу.
Зазначимо, що обертання може відбуватися не тільки з позитивним прискоренням, але і негативним. У цьому випадку у формулах другого рядка слід перед другим доданком поставити знак мінус.
Приклад розв’язання задачі
На металевий вал протягом 10 секунд діяв момент сили 1000 Н*м. Знаючи, що момент інерції вала дорівнює 50 кг*м2, необхідно визначити кутову швидкість, яку надав валу згаданий момент сили.
Застосовуючи основне рівняння обертання, обчислимо прискорення вала:
M = I*α =>
α = M/I.
Оскільки це кутове прискорення діяло на вал протягом часу t = 10 секунд, то для обчислення кутової швидкості застосовуємо формулу равноускоренного руху:
ω = ω0 + α*t = M/I*t.
Тут ω0 = 0 (вал не обертався до дії моменту сил M).
Підставляємо в рівність чисельні значення величин, отримуємо:
ω = 1000/50*10 = 200 рад/с.
Щоб це число перевести у звичні обертів в секунду, його необхідно поділити на 2*pi. Виконавши цю дію, отримуємо, що вал буде обертатися з частотою 31,8 про./с.
