Лінійна алгебра, яка викладається у вузах на різних спеціальностях, об’єднує чимало складних тем. Одні з них пов’язані з матрицями, а також з рішенням систем лінійних рівнянь методами Гаусса і Гаусса – Жордана. Не всім студентам вдається зрозуміти ці теми, алгоритми розв’язання різних завдань. Давайте разом розберемося в матрицях і методи Гаусса і Гаусса – Жордана.
Основні поняття
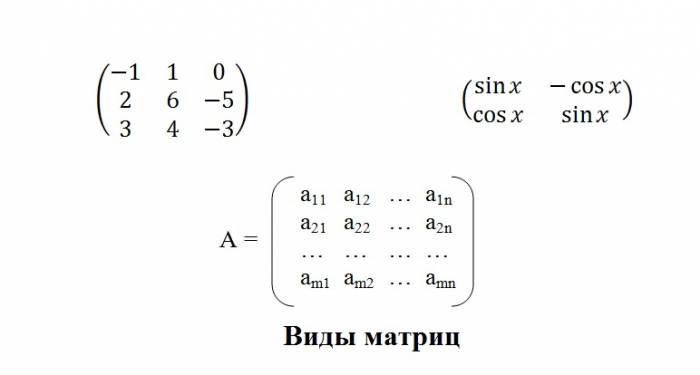
Під матрицею в лінійній алгебрі розуміється прямокутний масив елементів (таблиця). Нижче представлені набори елементів, укладені в круглі дужки. Це і є матриці. З наведеного прикладу видно, що елементами в прямокутних масивах є не тільки числа. Матриця може складатися з математичних функцій, алгебраїчних символів.
Для того щоб розібратися з деякими поняттями, складемо матрицю A з елементів aij. Індекси є не просто літерами: i – номер рядка в таблиці, а j – номер стовпця, в області перетину яких розташований елемент aij. Отже, ми бачимо, що у нас вийшла матриця з таких елементів, як a11, a21, a12, a22 і т. д. Буквою n ми позначили число стовпців, а буквою m – число рядків. Символ m × n означає розмірність матриці. Це те поняття, яке визначає кількість рядків і стовпців в прямокутному масиві елементів.
Необов’язково в матриці повинно бути декілька стовпців і рядків. При розмірності 1 × n масив елементів є однострочным, а при розмірності m × 1 – одностолбцовым. При рівності числа числа рядків і стовпців матрицю називають квадратною. У кожної квадратної матриці є визначник (det A). Під цим терміном розуміється число, яке ставиться у відповідність матриці A.
Ще кілька важливих понять, які треба запам’ятати для успішного вирішення матриць, – це головна і побічна діагоналі. Під головною діагоналлю матриці розуміється та діагональ, яка іде вниз у правий кут таблиці з лівого кута зверху. Побічна діагональ йде в правий кут вгору з лівого кута знизу.