Пряма трикутна призма. Формули об’єму та площі поверхні. Рішення геометричної задачі

В старших класах шкіл після вивчення властивостей фігур на площині переходять до розгляду просторових геометричних об’єктів таких, як призми, сфери, піраміди, циліндри та конуси. У цій статті дамо максимально повну характеристику прямої трикутної призми.

Що собою являє трикутна призма?

Почнемо статтю з визначення фігури, про яку далі піде мова. Призма з точки зору геометрії є фігурою в просторі, утвореної двома однаковими n-косинцями, що знаходяться в паралельних площинах, однакові кути яких з’єднані прямими відрізками. Ці відрізки називаються бічними ребрами. Разом зі сторонами основи вони утворюють бічну поверхня, яка в загальному випадку представлена параллелограммами.

Два n-кутника – це підстави фігури. Якщо бічні ребра перпендикулярні їм, то говорять про прямий призми. Відповідно, якщо число сторін багатокутника n у підставах дорівнює трьом, то така фігура називається трикутною призмою.

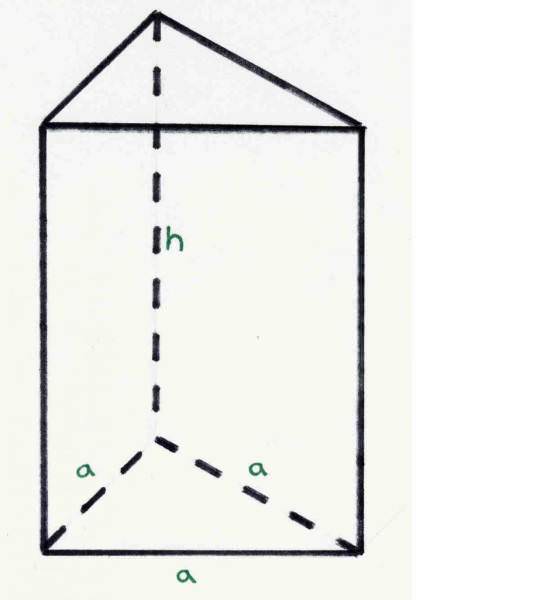
Трикутна пряма призма показано вище на малюнку. Ця фігура також називається правильною, оскільки в її основах лежать рівносторонні трикутники. Довжина бічного ребра фігури, позначена на рисунку буквою h, називається її висотою.

Малюнок показує, що призма з трикутним підставою утворена п’ятьма гранями, дві з яких – рівносторонні трикутники, а три – однакові прямокутники. Крім граней, призма володіє шістьма вершинами при підставах і дев’ятьма ребрами. Кількості розглянутих елементів пов’язані один з одним теоремою Ейлера:

число ребер = кількість вершин + кількість сторін – 2.

Площа прямої трикутної призми

Вище ми з’ясували, що розглянута фігура утворена п’ятьма гранями двох видів (два трикутника, три прямокутника). Всі ці грані утворюють повну поверхню призми. Їх сумарна площа є площею фігури. Нижче показана розгортка трикутної призми, яка може бути отримана, якщо від фігури спочатку відрізати дві підстави, а потім, розрізати вздовж одного ребра і розгорнути бічну поверхню.

Наведемо формули для визначення площі поверхні цієї розгортки. Почнемо з підстав прямої трикутної призми. Оскільки представляють вони трикутники, то площа S3 кожного з них може бути знайдена так:

S3 = 1/2*a*ha.

Тут a – це сторона трикутника, ha – опущена з вершини трикутника висота на цю сторону.

Якщо трикутник є рівностороннім (правильним), то формула для S3 залежить лише від одного параметра a. Вона має вигляд:

S3 = √3/4*a2.

Цей вираз можна отримати, якщо розглянути прямокутний трикутник, утворений відрізками a, a/2, ha.

Площа підстав So для правильної фігури в два рази більше величини S3:

So = 2*S3 = √3/2*a2.

Що стосується площі бічної поверхні Sb, то обчислити її не складно. Для цього досить помножити на три площа одного прямокутника, утвореного сторонами a і h. Відповідна формула має вигляд:

Sb = 3*a*h.

Таким чином, площа призми з підставою трикутним знаходиться по наступній формулі:

S = So + Sb = √3/2*a2 + 3*a*h.

Якщо призма є прямий, але неправильної, тоді для розрахунку площі слід окремо складати площі прямокутників, які один одного не будуть рівні.

Визначення обсягу фігури

Під обсягом призми розуміють обмежене її сторонами (гранями) простір. Розрахувати обсяг прямої трикутної призми набагато простіше, ніж площа її поверхні. Для цього достатньо знати площа основи і висоту фігури. Оскільки висотою h прямий фігури є довжина її бічного ребра, а як розраховувати площа підстави, ми привели у попередньому пункті, то залишається помножити одне на одного ці дві величини, щоб отримати потрібний об’єм. Формула для нього приймає вигляд:

V = S3*h.

Зазначимо, що твори площі однієї підстави на висоту дасть обсяг не тільки прямої призми, але також похилій фігури і навіть циліндра.

Рішення завдання

Скляні трикутні призми використовують в оптиці для вивчення спектра електромагнітного випромінювання завдяки явища дисперсії. Відомо, що скляна правильна призма має довжину сторони основи 10 см і довжину ребра 15 див. Чому дорівнює площа її скляних граней, і який обсяг у собі вона містить?