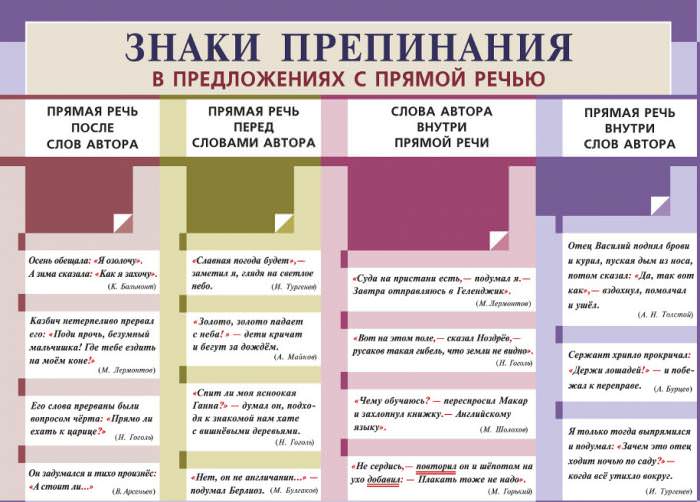
При вивченні абсолютно будь-просторової фігури важливо знати, як розраховувати її обсяг. У даній статті наводиться формула обсягу правильної чотирикутної піраміди, а також на прикладі розв’язання задач показано як цією формулою слід користуватися.
Про який піраміді піде мова?
Кожному школяреві старших класів відомо, що піраміда являє собою многогранник, який складається з трикутників і багатокутника. Останній є підставою фігури. Трикутники мають одну спільну сторону з підставою і перетинаються в єдиній точці, яка є вершиною піраміди.
Кожна піраміда характеризується довжиною сторін підстави, довжиною бічних ребер і висотою. Остання являє собою перпендикулярний відрізок, опущений з вершини до основи фігури.
Правильна чотирикутна піраміда являє собою фігуру з квадратною основою, висота якої перетинає цей квадрат в його центрі. Мабуть, найвідомішим прикладом пірамід цього типу є стародавні єгипетські кам’яні будови. Нижче наведена фотографія піраміди Хеопса.

Вивчається фігура має п’ять граней, чотири з яких – це однакові рівнобедрені трикутники. Також вона характеризується п’ятьма вершинами, чотири з яких належать підстави, і вісьмома ребрами (4 ребра підстави і 4 ребра бічних граней).
Формула обсягу правильної чотирикутної піраміди
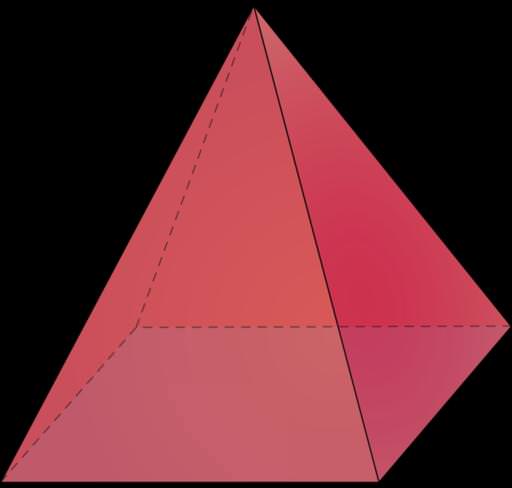
Обсяг даної фігури являє собою частину простору, що обмежують п’ять сторін. Щоб обчислити цей обсяг скористаємося наступною залежністю площі паралельного основи піраміди зрізу Sz від вертикальної координати z:
Sz = So * (h – z/h)2
Тут So – площа квадратного підстави. Якщо записане вираз підставити z = h, то ми отримаємо нульове значення для Sz. Цій величині z відповідає зріз, який буде містити тільки вершину піраміди. Якщо ж z = 0, то ми отримуємо значення площі підстави So.

Об’єм піраміди знайти нескладно, знаючи функцію Sz(z), для цього достатньо розрізати фігуру на нескінченне число паралельних основи шарів, а потім провести операцію інтегрування. Іду цією методикою, отримуємо:
V = ∫0h(Sz)*dz = -S0*(h-z)3 / (3*h 2)|0h = 1/3*S0*h.
Оскільки S0 – площа квадратного підстави, то, позначивши сторону квадрата буквою a, отримуємо формулу обсягу правильної чотирикутної піраміди:
V = 1/3*a2*h.
Тепер покажемо на прикладах розв’язання задач, як слід застосовувати цей вислів.
Завдання на визначення обсягу піраміди через її апофему і бічне ребро
Апофемой піраміди називають висоту її бічного трикутника, яка опущена на сторону основи. Оскільки всі трикутники рівні в правильній піраміді, то їх апофемы також будуть однаковими. Позначимо її довжину символом hb. Бічне ребро позначимо як b.
Знаючи, що апофема піраміди дорівнює 12 см, а бічне ребро дорівнює 15 см, знайдіть об’єм правильної чотирикутної піраміди.
Записана в попередньому пункті формула для об’єму фігури містить два параметри: довжину сторони a і висоту h. На даний момент нам не відомий жоден з них, тому займемося їх обчисленнями.
Довжину сторони квадрата a нескладно розрахувати, якщо скористатися теоремою Піфагора для прямокутного трикутника, у якого є гіпотенузою ребро b, а катетами будуть апофема hb і половина сторони підстави a/2. Отримуємо:
b2 = hb2 + a2/4 =>
a = 2*√(b2 – hb2).
Підставляючи відомі значення з умови, отримаємо величину a = 18 див.
Щоб обчислити висоту h піраміди, можна зробити двома способами: розглянути прямокутний трикутник з гіпотенузою-бічним ребром або з гіпотенузою-апофемой. Обидва способи рівноправні і передбачають виконання одного і того ж кількості математичних операцій. Зупинимося на розгляді трикутника, де є гіпотенузою апофема hb. Катетами в ньому будуть h і a/2. Тоді отримуємо:
h = √(hb2-a2/4) = √(122 – 182/4) = 7,937 див.
Тепер можна скористатися формулою для об’єму V:
V = 1/3*a2*h = 1/3*182*7,937 = 857,196 см3.
Таким чином, об’єм правильної чотирикутної піраміди дорівнює приблизно 0,86 літра.
Об’єм піраміди Хеопса
Тепер вирішимо цікаву і практично важливе завдання: знайдемо, чому дорівнює обсяг самої великої піраміди в Гізі. З літературних даних відомо, що вихідна висота будівлі була дорівнює 146,5 метра, а довжина його заснування становить 230,363 метра. Ці цифри дозволяють застосувати формулу для обчислення V. Отримуємо:
V = 1/3*a2*h =1/3*230,3632*146,5 ≈ 2591444 м3.
Отримане значення становить майже 2,6 млн. м3. Цей обсяг відповідає об’єму куба, сторона якого дорівнює 137,4 метра.