У шкільному курсі фізики велика увага приділяється опису кінематики і динаміки поступального руху тіл у тривимірному просторі. Але обертальний рух грає не менш важливу роль в техніці і природі. У цій статті розглянемо, що розуміють під моментом інерції тіла при його обертанні навколо осі.
Динаміка обертання
Перш ніж давати визначення моменту інерції тіла, розповімо, для чого потрібна ця величина і в яких рівняннях вона з’являється. В першу чергу, це головне рівняння динаміки обертання – формула моментів. Записується вона так:
M = I*α.
Тут M, α I – це момент сили, кутове прискорення і момент інерції, відповідно. По суті, це рівняння можна назвати другим ньютонівським законом для обертального руху. Нескладно здогадатися, що величина I тут грає ту ж саму роль, що інерційна маса в разі поступального руху.
Крім наведеного рівняння, існує ще одна важлива формула, яка застосовується часто для вирішення завдань на обертання тіл – це закон збереження моменту імпульсу. Його, як правило, записують в такій зручній для практики формі:
I*ω = const.
Як бачимо, тут момент інерції теж є ключовою величиною, ω – це кутова швидкість.
Момент інерції твердого тіла
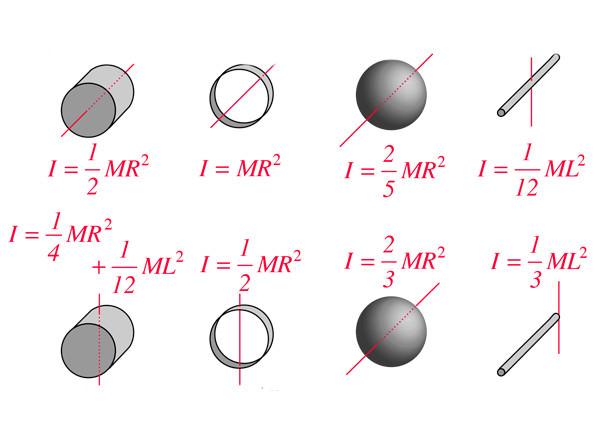
Тепер настав час дати визначення величиною I. Спочатку розглянемо його для матеріальної точки. Її моментом інерції називається добуток маси на квадрат відстані до осі обертання. Якщо масу позначити буквою m, а дистанцію до осі від точки буквою r, то формула для I запишеться так:
I = m*r2.
Як видно, I виражається в кг*м2. Рівність для точки можна використовувати для визначення моменту інерції тіла відносно осі. В цьому випадку застосовують наступне інтегральне вираження:
I = ∫m(r2*dm).
Ця формула застосовується для обчислення величин I абсолютно будь-яких систем з різними геометричними формами. Останнє рівність також використовують при вирішенні практичних завдань в наступному вигляді:
I = ∫V(ρ*r2*dV).
Де ρ – густина речовини. Нижче в статті покажемо, як використовувати інтегральне рівняння для вирішення конкретних завдань.
Величина I для циліндра
Кожен школяр уявляє собі фігуру “циліндр”. По правді кажучи, вони бувають найрізноманітнішими (еліптичними, гиперболическими, похилими). Тут розглянемо найпростіший випадок. Це прямий круговий циліндр, який обмежене циліндричною поверхнею і двома однаковими колами. Вісь обертання фігури проходить через її центр мас і через центри обох підстав. Обчислимо щодо неї момент інерції тіла.

Запишемо вихідну формулу:
I = ∫V(ρ*r2*dV).
Щоб її застосувати, уявімо собі циліндр у вигляді тонко нарізаних круглих однакових шарів. Позначимо їх товщину dl, радіус фігури дорівнює R, а висота – L. Тепер кожен тонкий шар об’ємом pi*R2*dl разрежем на безліч кілець, товщина кожного з яких дорівнює dr. Після виконання всіх описаних уявних геометричних операцій можна записати формулу для елементарного об’єму dV, тобто для обсягу одного кільця:
dV = 2*pi*r*dr*dl.
В результаті цього подання вихідний вираз для I перетворюється у формулу з подвійним інтегралом:
I = ∫L∫R(ρ*r2*2*pi*r*dr*dl) = 2*pi*ρ*L*R4/4 = M*R2/2.
Де буквою M зазначена маса всього циліндра.
Таким чином, ми отримали кінцевий вираз для моменту інерції циліндра. Як видно, він визначається тільки радіусом фігури та її масою і не залежить від довжини (висоти). Останнє означає, що аналогічну формулу можна застосовувати для визначення величини I для диска будь-якої товщини.
Величина I для стрижня
Тепер застосуємо формулу для визначення моменту інерції тонкого стержня. Принциповим моментом тут є той факт, що його товщина повинна бути набагато менше довжини L. Масу стержня позначимо літерою M. Момент інерції розрахуємо для положення осі, яка проходить через центр мас тіла і перпендикулярна йому.
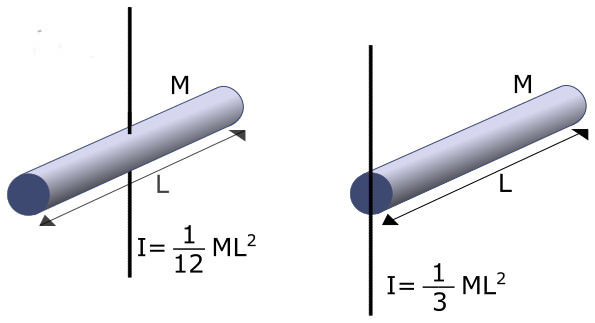
Почнемо розрахунок все з тієї ж формули, що і у випадку з циліндром:
I = ∫V(ρ*r2*dV).
Подумки разрежем весь стрижень на тонкі шари. Позначимо площу перерізу кожного з них S, а його товщину – dl. Тоді отримуємо формулу для dV:
dV = S*dl.
Тепер можна обчислити момент інерції тіла:
I = ∫-L/2+L/2(ρ*S*l2*dl).
Зауважимо, що кожен шар знаходиться від осі обертання на відстані l, тому ми замінили літеру r. Крім того, звертаємо увагу на межі інтегрування, які мають таке значення тому, що вісь проходить точно через середину стрижня. В результаті отримуємо:
I = ∫-L/2+L/2(ρ*S*l2*dl) = ρ*S*l3/3|-L/2+L/2 = M*L2/12.
За допомогою аналогічних міркувань і обчислень можна показати, що якщо вісь обертання проходить через який-небудь кінець стрижня, то його момент інерції буде в чотири рази більше, тобто:
I = M*L2/3.
Фізичний зміст величини
Вище ми вже сказали кілька слів про те, що означає момент інерції тіла з фізичної точки зору. Тут зупинимося дещо детальніше на цьому питанні.
Якщо уважно подивитися на формулу для I, то можна побачити, що ця величина залежить не тільки від самої маси тіла, але і від її розподілу, тобто від форми тіла, а також від його положення відносно осі обертання.
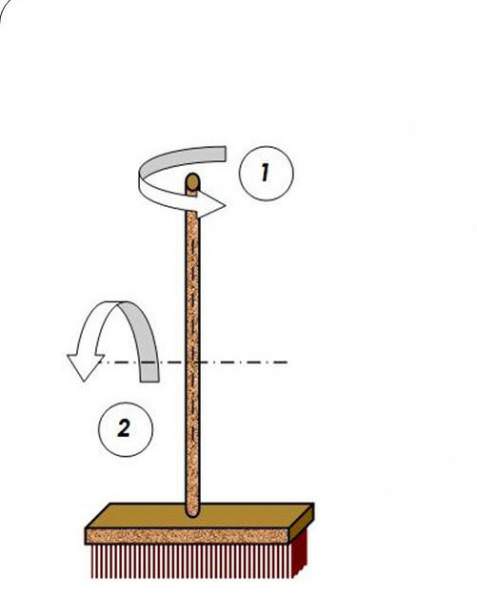
Яскравим прикладом є звичайна швабра або просто стрижень. Кожна людина хоч раз у житті розкручував швабру навколо осі, що проходить уздовж її ручки або перпендикулярно їй. У першому випадку легкого руху долонь достатньо, щоб надати кутове прискорення швабрі, у другому ж – доводиться докладати деяку силу рук, щоб розкрутити її. Пояснити цей факт просто. У першому випадку момент інерції практично дорівнює нулю, у другому – він має деяку кінцеву величину.