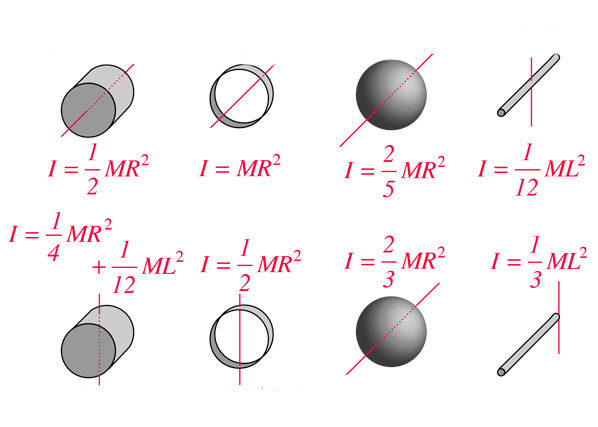Піраміда є досконалою геометричною фігурою, форму якої можна зустріти в деяких предметах з нашого життя, наприклад, в магічні амулети. У цій статті розглянемо, як знайти площу правильної трикутної піраміди і наведемо відповідну формулу.
Трикутна піраміда, тетраедр або
В геометрії пірамідою називають такий геометричний об’єкт, який складається з n трикутників і одного n-кутника. Всі трикутники перетинаються в точці, яка називається вершиною фігури, а n-кутник є її підставою. Не складно здогадатися, що назва піраміди визначається числом сторін n-кутника.
У відповідності з темою даної статті, ми розглянемо трикутну піраміду. Її n-вугільним підставою є також трикутник. Тому така піраміда складається з 4 трикутних граней, кожну з яких можна розглядати в якості підстави. У трикутної піраміди 4 рівноправних вершини і 6 ребер. Оскільки число сторін фігури дорівнює 4, то її також називають тетраедром. Для наочності наведемо зображення трикутної піраміди:

На малюнку показаний вид зверху на фігуру.