Усі тіла, які оточують нас, знаходяться в постійному русі. Переміщення в просторі тел спостерігається на всіх масштабних рівнях, починаючи з руху елементарних частинок в атомах речовини і закінчуючи прискореним рухом галактик у Всесвіті. У будь-якому випадку процес руху відбувається з прискоренням. У цій статті докладно розглянемо поняття стосовного прискорення і наведемо формули, за якою його можна розрахувати.
Кінематичні величини
Перш ніж вести розмову про дотичному прискоренні, розглянемо, якими величинами прийнято характеризувати довільне механічне переміщення тіл у просторі.
В першу чергу — це шлях L. Він показує, яку відстань в метрах, сантиметрах, кілометрах і так далі пройшло тіло за певний проміжок часу.
Друга важлива характеристика в кінематиці — це швидкість тіла. На відміну від шляху, вона є величиною векторною і спрямована вздовж траєкторії руху тіла. Швидкість визначає швидкість зміни просторових координат у часі. Формула для обчислення має вигляд:
v = dL/dt
Швидкість – це похідна по часу шляху.
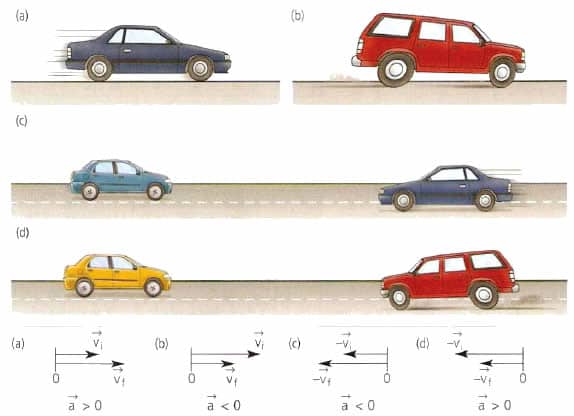
Нарешті, третьою важливою характеристикою руху тіл є прискорення. Згідно з визначенням у фізиці, прискорення — це величина, яка визначає зміну швидкості від часу. Формулу можна записати у вигляді:
a = dv/dt
Прискорення, як і швидкість, теж є величиною векторною, проте на відміну від неї воно спрямоване у бік зміни швидкості. Напрямок прискорення також збігається з вектором результуючої сили, що надає дію на тіло.