Вивченням характеристик тривимірних геометричних фігур займається стереометрія. Одна з відомих об’ємних фігур, яка з’являється в задачах геометрії, – це пряма призма. Розглянемо в цій статті, що вона собою являє, а також детально охарактеризуємо призму з трикутною основою.
Призма і її види
Під призмою мають на увазі таку фігуру, яка утворюється в результаті паралельного перенесення багатокутника в просторі. В результаті цієї геометричної операції утворюється фігура, що складається з кількох паралелограмів і двох однакових паралельних один одному багатокутників. Паралелограми є боковими сторонами призми, а багатокутники – це її заснування.
Будь-яка призма має n+2 сторони, 3*n ребер і 2*n вершин, де n – число кутів сторін або багатокутного підстави. На зображенні показана п’ятикутна призма, яка складається з 7 сторін, 10 вершин і 15 ребер.
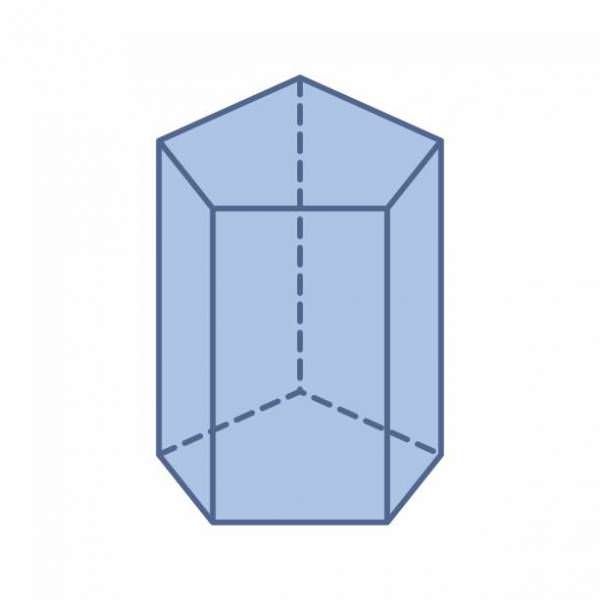
Розглянутий клас фігур представлений призмами декількох видів. Коротко перелічимо їх:
- увігнуті і опуклі;
- похилі і прямі;
- неправильні і правильні.
Кожна фігура відноситься до одного з перерахованих трьох видів класифікації. Під час розв’язування геометричних задач найпростіше виконувати розрахунки для правильних і прямих призм. Останні детальніше розглянемо в наступних пунктах статті.
Що це – пряма призма?
Прямою називається увігнута або опукла, правильна чи неправильна призма, у якої всі бічні сторони представлені чотирикутниками з кутами 90°. Якщо хоча б один з чотирикутників бічних сторін не буде прямокутником або квадратом, то призма називається похилою. Можна дати інше визначення: пряма призма – це така фігура даного класу, у якої будь-бічне ребро дорівнює висоті. Під висотою h призми вважають дистанцію між її підставами.
Обидва наведених визначення того, що це – пряма призма, є рівноправними і самодостатніми. З них випливає, що всі двогранні кути між будь-яким з підстав і кожної бічною стороною дорівнюють 90°.
Вище було сказано, що з прямими фігурами зручно працювати при вирішенні завдань. Це пов’язано з тим, що висота збігається з довжиною бічного ребра. Останній факт полегшує процес обчислення об’єму фігури і площі його бічної поверхні.
Об’єм прямої призми
Обсяг – властива будь-просторової фігури величина, яка чисельно відображає частину простору, укладеного між поверхнями розглянутого об’єкта. Обсяг призми може бути розрахований за такою загальною формулою:
V = So*h.
Тобто добуток висоти на площу основи дасть шукане значення V. Оскільки у прямої призми підстави рівні, то для визначення площі So можна брати будь-яке з них.
Перевага використання наведеної вище формули саме для прямої призми в порівнянні з іншими її видами полягає в тому, що висоту фігури знайти дуже просто, так як вона збігається з довжиною бічного ребра.
Площа бічної поверхні
Зручно розраховувати не тільки обсяг для прямої фігури розглянутого класу, але також її бічну поверхню. Дійсно, будь-яка її бічна сторона – це або прямокутник або квадрат. Як обчислити площу цих плоских фігур, знає кожен школяр, для цього необхідно помножити суміжні сторони один на одного.
Припустимо, що в основі призми лежить довільний n-кутник, сторони якого дорівнюють ai. Індекс i пробігає значення від 1 до n. Площа одного прямокутника обчислюється так:
Si = ai*h.
Площа поверхні бічної Sb неважко обчислити, якщо скласти всі площі Si прямокутників. У такому разі отримуємо кінцеву формулу для Sb прямої призми:
Sb = h*∑i=1n(ai) = h*Po.
Таким чином, щоб визначити площу бічної поверхні прямої призми, необхідно помножити її на висоту периметр однієї підстави.
Завдання з трикутною призмою
Припустимо, що задана пряма призма. Основа – прямокутний трикутник. Катети цього трикутника дорівнюють 12 см і 8 див. Необхідно розрахувати обсяг фігури і її повну площу, якщо висота призми становить 15 див.
Для початку обчислимо об’єм прямої призми. Трикутник (прямокутний), що знаходиться в її основах, має площу:
So = a1*a2/2 = 12*8/2 = 48 см2.
Як можна здогадатися, a1 і a2 в цьому рівність є катетами. Знаючи площу основи і висоту (див. умову задачі), можна скористатися формулою для V:
V = So*h = 48*15 = 720 см3.
Повна площа фігури утворена двома частинами: площами підстав і бічною поверхнею. Площі двох підстав рівні:
S2o = 2*So = 48*2 = 96 см2.
Для обчислення площі бічної поверхні необхідно знати периметр прямокутного трикутника. Обчислимо за теоремою Піфагора його гіпотенузу a3, маємо:
a3 = √(a12 + a22) = √(122 + 82) = 14,42 див.
Тоді периметр трикутника підстави прямої призми складе:
P = a1 + a2 + a3 = 12 + 8 + 14,42 = 34,42 див.
Застосовуючи формулу для Sb, яка була записана в попередньому пункті, отримуємо:
Sb = h*P = 15*34,42 = 516,3 див.
Склавши площі S2o і Sb, ми отримаємо повну площу поверхні досліджуваної геометричної фігури:
S = S2o + Sb = 96 + 516,3 = 612,3 см2.
Трикутна призма, яку виготовляють із спеціальних видів скла, застосовується в оптиці при вивченні спектрів випромінюючих світло об’єктів. Такі призми здатні розкладати світло на складові частоти завдяки явища дисперсії.
