При вивченні характеристик просторових фігур в курсі стереометрії велика увага приділяється таким властивостям, як площа і об’єм. В той же час знати лінійні параметри фігур важливо, щоб мати можливість розрахувати зазначені властивості. У даній статті відповімо на питання, як знайти апофему піраміди правильної трикутної.
Яка фігура буде розглянута?
Трикутна піраміда з правильним підставою являє собою фігуру в просторі, яка обмежена одним рівностороннім трикутником (заснування) та трьома равнобедренными трикутниками (бокові сторони). Щоб мати можливість більш чітко уявити цю піраміду, покажемо її на малюнку.
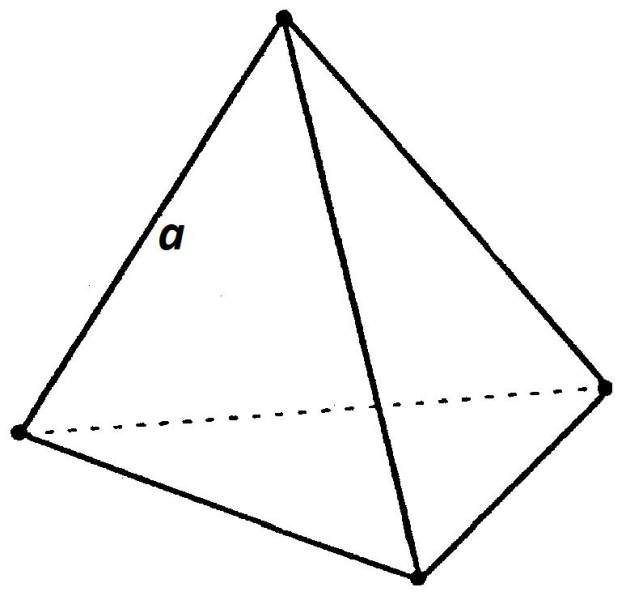
Важливою точкою будь піраміди є її вершина, яка не належить основи. Якщо опустити перпендикуляр з неї на підставу, то його довжина буде заввишки фігури. Надалі будемо позначати висоту буквою h. Висота правильної піраміди падає точно в геометричний центр трикутника (точка перетину його медіан, а також бісектрис і висот). Другим лінійним параметром, який слід знати, довжина сторони основи трикутної піраміди, тобто довжина сторони рівностороннього трикутника. Позначимо її буквою a.
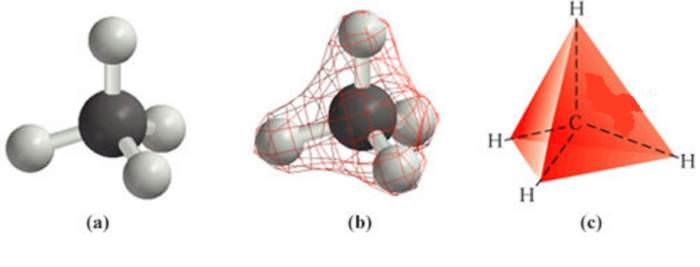
Трикутна піраміда має власну назву – тетраедр. Тетраедр не є чисто теоретичною геометричною фігурою. Вона також зустрічається в деяких природних структурах. Так, атом вуглецю в алмазі з’єднаний з чотирма такими ж атомами, що утворюють тетраедр. Інший приклад – це молекула метану, в якій вуглець, з’єднаний з чотирма атомами водню, утворює правильну трикутну піраміду.