Фігура конус є об’єктом вивчення стереометрії. Основними властивостями конуса є наявність у нього обсягу і площі поверхні, які можна обчислити за допомогою лінійних параметрів. Одним з них є діаметр конуса. У даній статті ми покажемо, як цей діаметр можна розрахувати за іншим відомим характеристикам фігури.
Круглий прямий конус
У загальному випадку конусом є фігура, побудована в результаті руху відрізку вздовж деякої кривої на площині, при цьому другий кінець відрізка зафіксований в певній точці простору. Сам відрізок називається генератрисой, або утворює, а крива – директрисою, або напрямної.
Згідно з наведеним визначенням, крива, яка обмежує фігуру, може бути абсолютно будь-якого типу. Найвідомішими з них є парабола, гіпербола, еліпс і окружність. В останньому випадку говорять про круглому конусі.
Круглий конус може бути похилим і прямим. Обидві фігури показано нижче на малюнку.
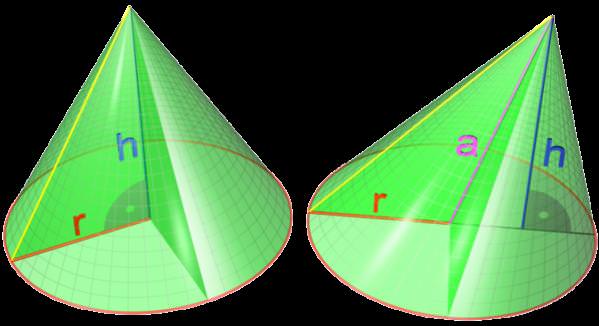
Тут r – радіус кола, що обмежує основа фігури. Буквою h позначена висота, яка представляє опущений на основу з вершини конуса перпендикуляр. Буквою a позначена вісь конуса. Видно, що у випадку прямої фігури його висота збігається з віссю, тобто перетинає коло в її центрі.
Крім радіусу r і висоти h, важливим лінійним параметром конуса є довжина його твірної g. Як було сказано, твірна – це відрізок, що з’єднує директрису з висотою. Для прямого круглого конуса все що утворюють рівні один одному.
Далі в статті, розкриваючи питання щодо того, як знайти діаметр конуса, буде розглядатися тільки конус круглий і прямий.