Що таке піраміда? Визначення піраміди, її основа, ребра, поверхню

Згадуючи величні споруди Древнього Єгипту, можна назвати піраміду самої таємничої геометричною фігурою. У цій статті дамо визначення піраміди. Піраміду також розглянемо з точки зору складових її елементів і її властивостей.

Що собою являє піраміда?

З точки зору стереометрії (геометрія тривимірного простору), можна дати наступне визначення піраміди: пірамідою називається тривимірна фігура, яка обмежена трикутними гранями і однієї багатокутної гранню. Дане визначення є досить простим і геометрично правильним. Тим не менш, вона не дозволяє ясно уявити собі, про яку фігуру йде мова.

Можна дати більш чітке визначення піраміди: піраміда – це фігура, яка виходить в результаті з’єднання прямими відрізками деякої точки у просторі з вершинами обраного багатокутника. Припустимо, що у нас є n-кутник (n – ціле число), розташоване в деякій площині. Виберемо довільну точку простору, яка не лежить у площині n-кутника. Для визначеності назвемо цю точку буквою H. Якщо з’єднати відрізками всі вершини n-кутника з точкою H, то ми отримаємо пірамідальну поверхню. Якщо до неї додати ще n-вугільне підстава, то утворена фігура буде пірамідою.

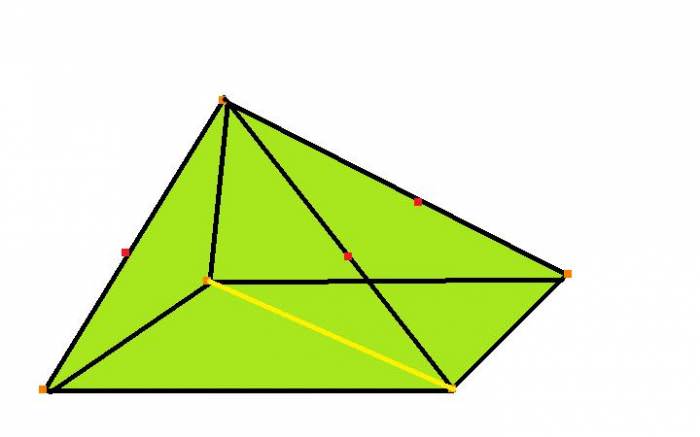
Вище схематичний малюнок демонструє чотирикутну піраміду довільного типу, побудовану за описаним вище способом.

З чого складається фігура?

Познайомившись з визначенням піраміди (піраміда в геометрії є полиэдром), можна переходити до розгляду елементів, якими вона утворена. Наведемо ще раз приклад піраміди.

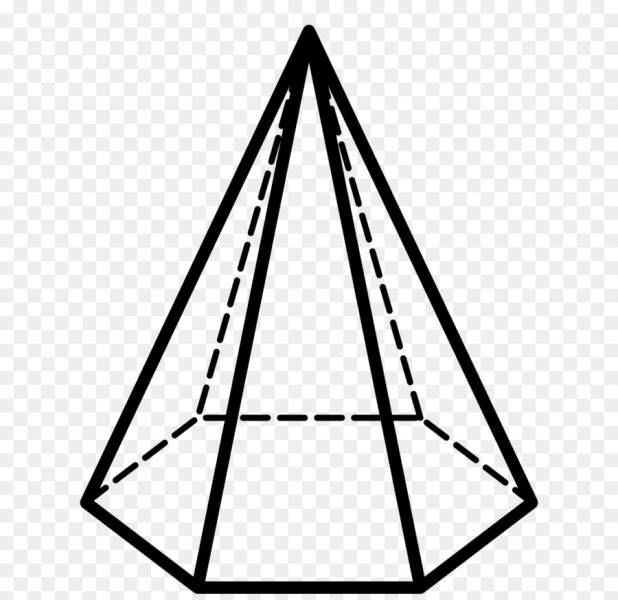
На цьому малюнку зображена шестикутна піраміда. Так вона називається по причині того, що в основі фігури розташований шестикутник. Глянувши на малюнок, можна виділити три основні геометричні елементи, які складають піраміду:

вершини;
ребра;
межі.

Почнемо характеристику фігури з вершин. Вони є “гострими” кінцями піраміди. Всього біля фігури n+1 вершина, що стає очевидним, якщо згадати про n вершинах підстави і одній точці H, не належить основи. Точка H є особливою вершиною фігури, оскільки вона бере участь у визначенні різних типів пірамід. Вершина H відрізняється від решти вершин тим, що в ній перетинаються всі n трикутників фігури.

Ребра – це відрізки, що з’єднують між собою вершини в єдину конструкцію. Ребра піраміди бувають двох типів: по-перше, це ребра підстави, кількість яких дорівнює n, по-друге, це ребра бічній поверхні, їх число також одно n. Таким чином, число ребер розглянутої фігури дорівнює 2*n.

Грані, або сторони – важливі елементи будь-якої піраміди, які надають фігурі об’ємний вигляд. Межі фігури, як і ребра, бувають двох типів: по-перше, це підстава піраміди, яке являє собою плоский багатокутник з n вершинами і n сторонами, по-друге, це трикутники бічній поверхні. Кількість трикутників будь піраміди дорівнює n. У підсумку розглянутий полиэдр складається з n+1 одній грані.

У середині XVIII століття вчений зі Швейцарії Леонард Ейлер опублікував в одному з своїх праць теорему, яка пов’язує кількості розглянутих елементів полиэдра в єдине рівність. Теорема свідчить: якщо взяти суму граней і вершин, а потім з неї відняти число 2, то виходить сума всіх ребер полиэдра. Для піраміди з n-вугільним підставою маємо:

2*n = (n+1) + (n+1) – 2

Прямі і похилі піраміди

При розгляді питання, що таке піраміда, вище було сказано, що в залежності від числа сторін (кутів) багатокутного підстави говорять про чотирикутної піраміди, п’ятикутні, трикутної і так далі.

Існує ще одна важлива класифікація цих фігур: вони можуть бути прямими і похилими. Якщо з вершини H фігури провести до основи перпендикуляр, то в деякій точці O він перетне підстава піраміди. Якщо точка O є геометричним центром n-кутника, значить, піраміда буде прямою. Якщо O цим центром не є, то піраміда буде похилою.

Зовнішнє розходження між цими типами фігур видно з першого погляду. Похила і пряма чотирикутні піраміди показано нижче.

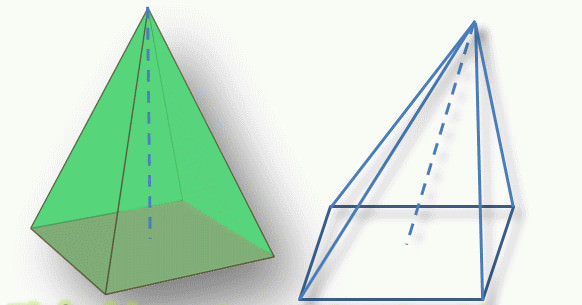
Правильні піраміди

Ще один важливий підклас пірамід – це правильні фігури. Правильної піраміда буде тільки в тому випадку, якщо для неї справедливі наступні два геометричних умови:

вона є прямою;
її основа – це n-кутник рівносторонній і равноугольный.

Що значить “піраміда пряма”, було зазначено в попередньому пункті. Тут пояснимо лише друга умова. Правильний багатокутник може мати скільки завгодно сторін, починаючи з 3-х. Так, правильними є рівносторонній трикутник, квадрат, шестикутник з однаковими довжинами сторін і кутами 120 o. Зауважимо, що ромб з однаковими сторонами не є правильним, оскільки у нього не всі кути рівні один одному.

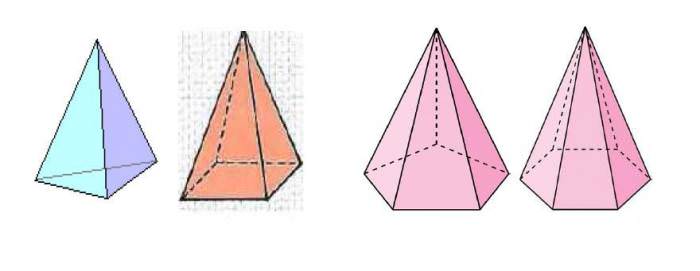
Вище показано чотири правильні піраміди, які володіють різними правильними підставами.

Будь-які математичні розрахунки параметрів зручно проводити саме для правильних фігур.

Параметри піраміди лінійні і кутові

Лінійні характеристики піраміди будь-якого типу дозволяють однозначно розрахувати будь-які інші властивості фігури. У стереометрії виділяють чотири типи лінійних параметрів:

довжина сторони підстави (якщо основа є неправильним, тоді необхідно для однозначності знати довжини всіх сторін і кути між ними);
висота;
довжина бічного ребра (ребер, якщо трикутники бічної поверхні не рівні один одному);
апофема фігури (висота бічної грані, проведена з вершини H).

Крім названих характеристик, в деяких завданнях також наводяться значення двогранних кутів між бічною гранню і підставою або лінійних кутів між бічним ребром і підставою.

У разі правильних пірамід існують конкретні математичні рівності, які пов’язують всі зазначені параметри.

Поверхню піраміди та її площу

Як відомо, розгляд площ просторових фігур прийнято та зручно здійснювати на прикладах їх плоских розгорток. Щоб показати, про що йде мова, нижче наведена розгортка для правильної п’ятикутної піраміди.

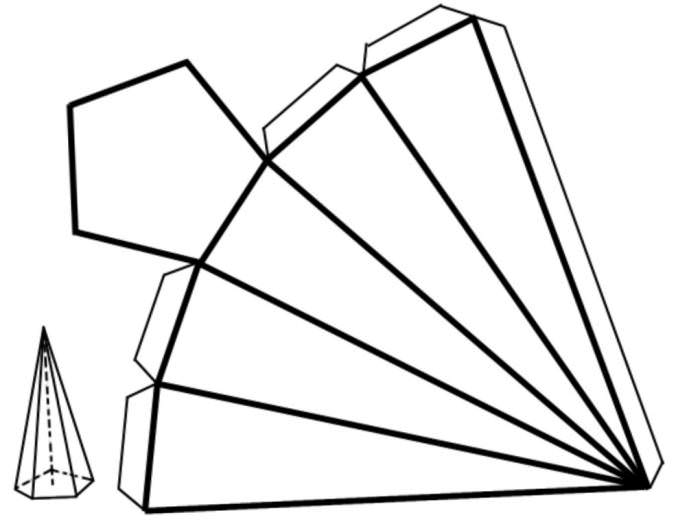
Оскільки всі грані піраміди представлені на площині, то розрахувати їх площа дуже просто, для цього слід скласти площі всіх n трикутників і площа одного n-кутника. Якщо всі сторони і кути названих фігур відомі, то вирішити поставлену задачу нескладно, якщо скористатися формулами для площі відповідної фігури.

Об’єм геометричної фігури

Оскільки піраміда має межі, то обмежуване ними обсяг простору є обсягом самої фігури. Для піраміди довільного типу розрахунок цієї величини виконується з використанням наступної формули:

V = 1/3*So*h

Тобто якщо взяти добуток висоти h на площу основи So, а потім отриманий результат розділити на три, то ми отримаємо обсяг фігури.

Для правильних пірамід V є функцією двох змінних: висоти h та сторони підстави a.

Рішення задачі на прикладі трикутної піраміди

Закріпимо отримані у статті знання, вирішивши таку задачу: відомо, що основу правильної трикутної піраміди має довжину 10 см, а висота фігури дорівнює 15 див. Чому дорівнюють обсяг і площа цієї піраміди?

Обчислимо спочатку площа підстави, яке є рівностороннім трикутником. Відповідна формула має вигляд:

So = √3/4*a2 = √3/4*102 = 43,3 см2

Тепер обчислимо апофему піраміди. Зробити це можна, якщо розглянути прямокутний трикутник, побудований на апофеме і висоті. Довжина апофемы hb обчислюється так: