Існує такий кумедний дитячий віршик, з допомогою якого легко запам’ятати, що таке бісектриса: “Бісектриса – це така криса, що бігає по кутах і ділить кут навпіл”. Однак не можна забувати, що, незважаючи на простоту запам’ятовування цього жартівливого визначення, вчитель справедливо зажадає інше, взяте з підручника.
В подальшому вивченні шкільної програми діти стикаються зі складною з першого погляду завданням – як побудувати биссектрису даного кута за допомогою циркуля. Проте вже більш просунутий школяр без праці впорається з цим завданням, яке є основою виконання циклу задач на побудову геометрії. Давайте ж розберемося з цим питанням раз і назавжди.
Як побудувати биссектрису даного кута?
Найбільш очевидним і найбільш простим способом є використання транспортира, але якщо цього допоміжного інструменту не виявилося під рукою, треба вміти будувати биссектрису без нього.
Для виконання даної задачі, як вже зрозумів читач, нам потрібно циркуль, а крім нього – лінійка (важливо розуміти, що на ній поділками користуватися не можна) і простий олівець з гумкою.
Алгоритм побудови
Необхідно здійснити такі дії:
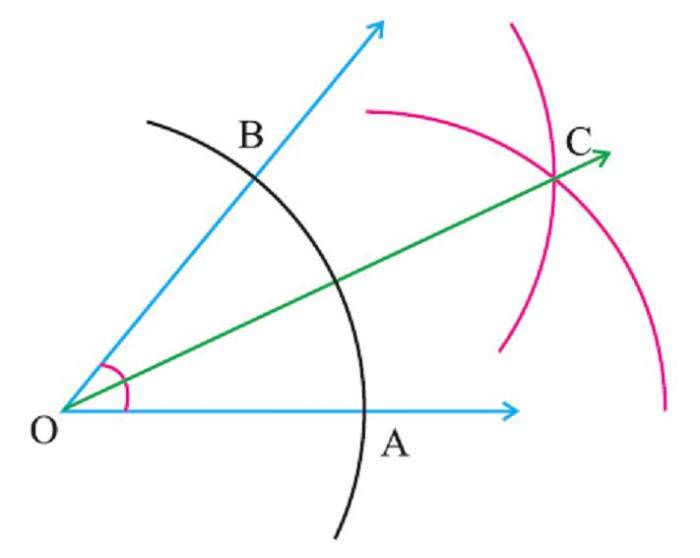
Ми дали відповідь на поставлене питання – як побудувати биссектрису даного кута.
Доказ
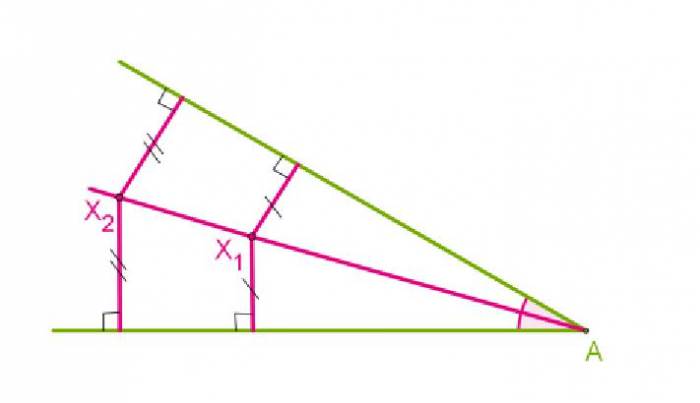
Тепер, розібравшись, як побудувати биссектрису даного кута, варто згадати ще одне визначення бісектриси, використовуючи термін “геометричне місце точок”. Бісектрисою називається геометричне місце точок, що рівновіддалені від променів, що утворюють кут.
Згідно виконаному побудови в пунктах 4-6, точка, що належить побудованої бісектрисі, також належить двом колах, рівним по радіусу, центр яких розташований на променях, що утворюють кут на однаковій відстані від вершини кута (згідно з пунктами 1-3 побудови). Опустимо перпендикуляр з зазначеної у пункті 6 точки на промені, що утворюють кут. Доведемо, що отримані прямокутні трикутники рівні, і з’ясуємо, що опущені перпендикуляри також рівні відповідні елементи трикутників. Таким чином, їх загальна гіпотенуза є бісектрисою кута за визначенням. Що і потрібно було довести.