Геометричні фігури у просторі є об’єктом вивчення стереометрії, курс якої проходять школярі в старших класах. Дана стаття присвячена такому досконалому многограннику, як призма. Розглянемо докладніше властивості призми і наведемо формули, які служать для їх кількісного опису.
Що це – призма?
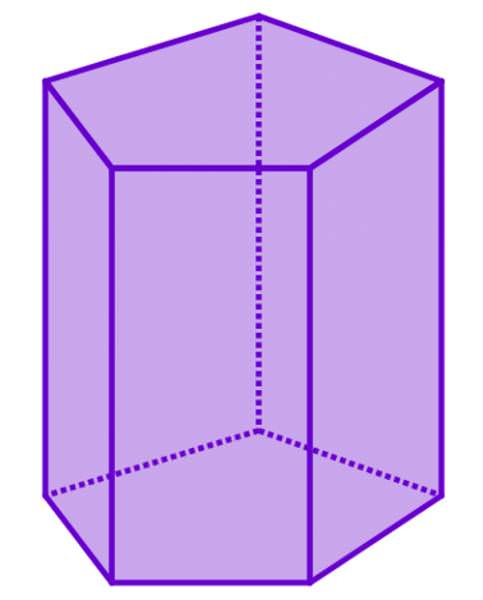
Кожен уявляє, як виглядає паралелепіпед або куб. Обидві фігури є призмами. Однак, клас призм набагато більш різноманітний. В геометрії цій фігурі дається наступне визначення: призмою є всякий багатогранник у просторі, який утворений двома паралельними і однаковими багатокутними сторонами і кількома параллелограммами. Однакові паралельні грані фігури називаються її підставами (верхнім і нижнім). Паралелограми ж – це бічні грані фігури, що з’єднують сторони підстави один з одним.
Якщо основа представлено n-кутником, де n – ціле число, тоді фігура буде складатися з 2+n граней, 2*n вершин і 3*(n) ребер. Грані і ребра відносяться до одного з двох типів: або вони належать бічній поверхні, яких підстав. Що стосується вершин, то всі вони є рівноправними і відносяться до основ призми.