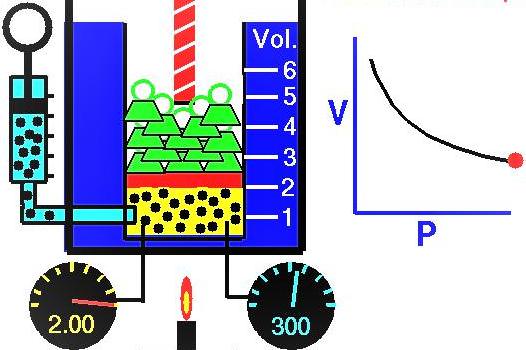
Будь-яке переміщення тіла в просторі, що призводить до зміни повної енергії, пов’язане з роботою. У цій статті розглянемо, що це за величина, що вимірюється механічна робота, і як вона позначається, а також вирішимо цікаву задачу по цій темі.
Робота як фізична величина
Перед тим як відповісти на питання, у чому вимірюється механічна робота, познайомимося з цією величиною. Згідно з визначенням, робота являє собою скалярний добуток сили на вектор переміщення тіла, що ця сила викликала. Математично можна записати наступне рівняння:
A = (F*S).
Круглі дужки вказують на скалярний добуток. Враховуючи його властивості, в явному вигляді ця формула перепишеться так:
A = F*S*cos(α).
Де α є кутом між векторами сили і переміщення.
Із записаних виразів випливає, що робота вимірюється в Ньютонах на метр (Н*м). Як відомо, ця величина називається джоулем (Дж). Тобто у фізиці механічна робота в одиницях роботи Джоулях вимірюється. Одному Джоулю відповідає така робота, при якій сила в один Ньютон, діючи паралельно переміщенню тіла, призводить до зміни його положення в просторі на один метр.
Що стосується позначення механічної роботи у фізиці, то слід зазначити, що для цього найчастіше користуються буквою A (від нім. ardeit – праця, робота). В англомовній літературі можна зустріти позначення цієї величини латинською буквою W. В російськомовній літературі ця буква зарезервована для позначення потужності.
Робота і енергія
Розбираючи питання, у чому вимірюється механічна робота, ми побачили, що її одиниці збігаються з такими для енергії. Це збіг не є випадковим. Справа в тому, що розглянута фізична величина є одним із способів прояву енергії в природі. Будь-яке переміщення тіл у силових полях або в їх відсутність вимагає енергетичних витрат. Останні йдуть на зміну кінетичної і потенційної енергії тел. Процес зміни характеризується виконуваної роботою.
Енергія є фундаментальною характеристикою тел. Вона зберігається в ізольованих системах, вона може перетворюватися в механічну, хімічну, теплову, електричну та інші форми. Робота ж є лише механічним проявом енергетичних процесів.
Робота в газах
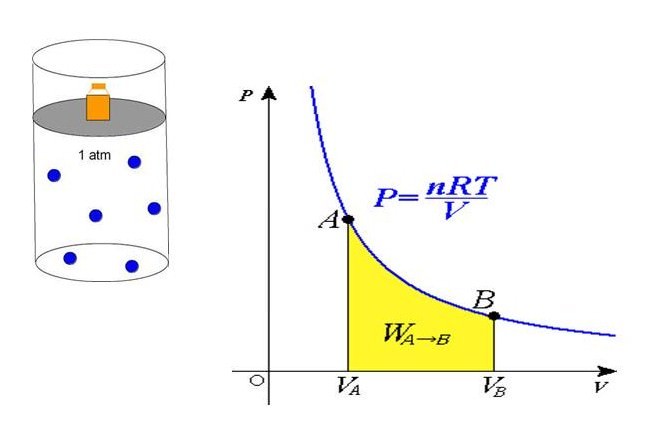
Записане вище вираз для роботи є базовим. Тим не менш, для вирішення практичних завдань з різних областей фізики ця формула може бути непридатна, тому користуються іншими виразами, отриманими на її основі. Одним з таких випадків є чинена газом робота. Її зручно розраховувати за наступною формулою:
A = ∫V(P*dV).
Тут P – тиск газу, V – його об’єм. Знаючи, у чому вимірюється механічна робота, легко довести справедливість інтегрального вирази, дійсно:
Па*м3 = Н/м2*м3 = Н*м = Дж.
У загальному випадку тиск – це функція обсягу, тому подынтегральное вираз може приймати довільний вигляд. У разі изобарного процесу розширення чи стиснення газу відбувається при постійному тиску. У цьому випадку робота газу дорівнює простому добутку величини P на зміну його обсягу.
Робота при обертанні тіла навколо осі

Рух обертання широко поширено в природі і в техніці. Воно характеризується поняттями моментів (сили, імпульсу та інерції). Щоб визначити роботу зовнішніх сил, які змусили тіло або систему обертатися навколо деякої осі, необхідно спочатку розрахувати момент сили. Обчислюється так:
M = F*d.
Де d – це відстань від вектора сили до осі обертання, воно називається плечем. Крутний момент M, який привів до повороту системи на кут θ навколо деякої осі, здійснює наступну роботу:
A = M*θ.
Тут M виражається в Н*м, а кут θ в радіанах.
Завдання з фізики на механічну роботу
Як було сказано в статті, робота завжди відбувається тією чи іншою силою. Розглянемо наступну цікаву задачу.
Тіло знаходиться на площині, що нахилена до горизонту під кутом 25o. Зсковзуючи вниз, тіло придбало певну кінетичну енергію. Необхідно розрахувати цю енергію, а також роботу сили тяжіння. Маса тіла дорівнює 1 кг, пройдений ним по площині шлях дорівнює 2 метри. Опором тертя ковзання можна знехтувати.
Вище було показано, що здійснює роботу тільки та частина сили, яка направлена вздовж переміщення. Неважко показати, що в даному випадку переміщення вздовж буде діяти наступна частина сили тяжіння:
F = m*g*sin(α).
Тут α – кут нахилу площини. Тоді робота обчислюється так:
A = m*g*sin(α)*S = 1*9,81*0,4226*2 = 8,29 Дж.
Тобто сила тяжіння робить позитивну роботу.
Тепер визначимо кінетичну енергію тіла в кінці спуску. Для цього згадаємо другий ньютонівський закон і розрахуємо прискорення:
a = F/m = g*sin(α).
Оскільки зсув тіла є рівноприскореним, то ми вправі скористатися відповідною кінематичної формулою для визначення часу руху:
S = a*t2/2 =>
t = √(2*S/a) = √(2*S/(g*sin(α))).
Швидкість тіла в кінці спуску розраховується так:
v = a*t = g*sin(α)*√(2*S/(g*sin(α))) = √(2*S*g*sin(α)).
Кінетична енергія поступального руху визначається за допомогою наступного виразу:
E = m*v2/2 = m*2*S*g*sin(α)/2 = m*S*g*sin(α).
Ми отримали цікавий результат: виявляється, формула для кінетичної енергії точно збігається з виразом для роботи сили тяжіння, яке було отримано раніше. Це свідчить про те, що вся механічна робота сили F спрямована на збільшення кінетичної енергії змінного тіла. В дійсності через сил тертя робота A завжди виявляється більше енергії E.