У шкільному курсі стереометрії вивчають властивості різних просторових фігур. Однією з них є піраміда. Дана стаття присвячена питанню про те, як знайти у площа бічної поверхні піраміди. Також розкривається питання визначення цієї площі для усіченої піраміди.
Що таке піраміда?
Багато хто, почувши слово “піраміда”, відразу уявляють грандіозні споруди Древнього Єгипту. Дійсно, гробниці Хеопса і Хефрена є правильними чотирикутними пірамідами. Тим не менш пірамідою також є тетраедр, фігури з п’яти-, шести-, n-вугільним підставою.
В геометрії поняття піраміди визначено чітко. Під цією фігурою розуміють об’єкт в просторі, який утворюється в результаті з’єднання деякої точки з кутами плоского n-кутника, де n – ціле число. Нижче малюнок показує чотири піраміди з різною кількістю кутів в підставі.
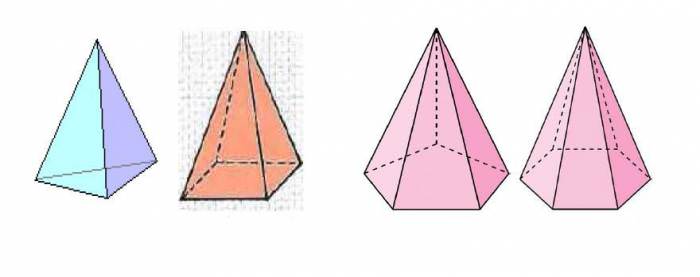
Точка, з якої з’єднані всі вершини кутів підстави, не лежить в його площині. Вона називається вершиною піраміди. Якщо з неї провести до основи перпендикуляр, то ми отримаємо висоту. Фігура, у якої висота перетинає основу в геометричному центрі, отримала назву прямої. Іноді пряма піраміда має правильне підставу, наприклад квадрат, рівносторонній трикутник і так далі. У цьому випадку вона називається правильною.
При обчисленні у піраміди площі бічної поверхні зручно працювати з правильними фігурами.