Обернені тригонометричні функції традиційно викликають труднощі у школярів. Уміння обчислювати тангенс числа може знадобитися в задачах ЄДІ з планіметрії і стереометрії. Для успішного вирішення рівняння і задачі з параметром необхідно мати уявлення про властивості функції арктангенса.
Визначення
Арктангенсом числа х називається таке число у, тангенс якого дорівнює х. Це є математичне визначення.
Функція арктангенса записується як y = arctg x.
У більш загальному вигляді: y = Carctg (kx + a).
Обчислення
Для розуміння того, як влаштована зворотна тригонометрична функція арктангенса, потрібно для початку згадати, як визначають значення тангенса числа. Розглянемо детальніше.
Тангенс х – це відношення синуса х до косинусу х. Якщо відома хоча б одна з цих двох величин, то другий модуль може бути отриманий з основного тригонометричного тотожності:
sin2 x + cos2 x = 1.
Правда, для розкриття модуля потрібно проведення оцінки.
Якщо ж відомо саме число, а не його тригонометричні характеристики, то в більшості випадків потрібно приблизно оцінити тангенс числа, звернувшись до таблиці Брадіса.
Винятки становлять так звані стандартні значення.
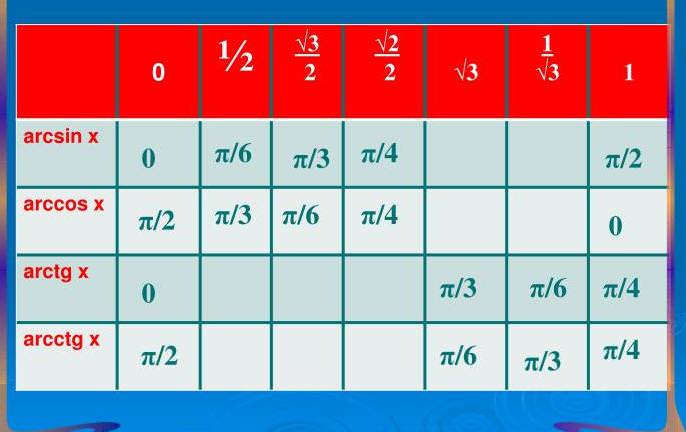
Вони представлені в наступній таблиці:
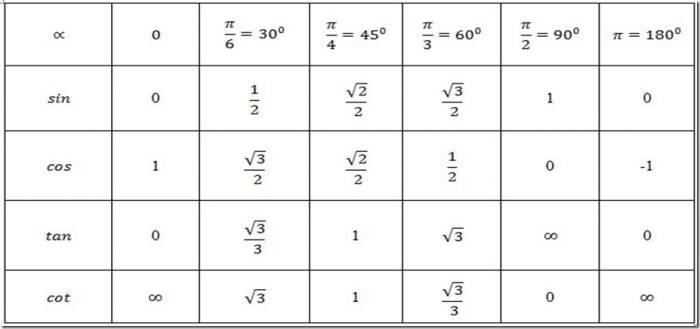
Крім перерахованих вище, стандартними можна вважати будь-які значення, отримані з даних додаванням числа виду ½пк (к – будь-яке ціле число, π=3,14).
Рівно те ж саме вірно і для арктангенса: найчастіше наближене значення можна подивитися по таблиці, а точно відомі лише декілька значень:
На практиці при вирішенні завдань шкільної математики прийнято давати відповідь у вигляді виразу, який містить тангенс, а не його приблизної оцінки. Наприклад, arctg 6, arctg (-¼).
Побудова графіка
Оскільки тангенс може приймати будь-які значення, область визначення функції арктангенса – вся числова пряма. Пояснимо докладніше.
Один і той же тангенс відповідає нескінченного числа аргументів. Наприклад, дорівнює нулю не тільки тангенс нуля, але і тангенс будь-якого числа виду π к, де к – ціле число. Тому математики домовилися вибирати для арктангенса значення з проміжку від -½ π до ½ π. Це потрібно розуміти так. Область значень функції арктангенса – інтервал (-½ π; ½ π). Кінці проміжку не включаються, так як тангенс -½п і ½п не існує.
На зазначеному інтервалі тангенс безперервно зростає. Отже, зворотна функція арктангенса теж є безперервно зростаючою на всій числовій прямій, але обмеженої зверху і знизу. Внаслідок цього вона має дві горизонтальні асимптоти y = -½ π y = ½ π.
У цьому випадку tg 0 = 0, інших точок перетину з віссю абсцис, крім (0;0), графік не може мати в силу зростання.
Як випливає з парності функції тангенса, тангенс має аналогічну властивість.
Для побудови графіка слід взяти кілька точок з числа стандартних значень:
Похідна функції y = arctg х в будь-якій точці обчислюється за формулою:
Зауважимо, що його похідна всюди додатна. Це узгоджується зі зробленим раніше висновком про безперервному зростанні функції.
Друга похідна арктангенса звертається до 0 в точці 0, негативна при позитивних значеннях аргументу і навпаки.
Це означає, що графік функції арктангенса має точку перегину в нулі і є опуклим вниз на проміжку (-∞; 0] і опуклим вгору на проміжку [0; +∞).
