З давніх часів людство прагнуло будь-якими способами полегшити свій фізична праця. Засобом для вирішення цієї проблеми стали прості механізми. У даній статті розглядаються такі винаходи, як важіль і блок, а також система важелів і блоків.
Що таке важіль і коли його почали застосовувати?
Ймовірно, кожен з дитинства знайомий з цим нехитрим механізмом. У фізиці важелем називається сукупність балки (стрижня, дошки) і однієї опори. Служить важіль для підняття вантажів або для сполучення швидкостей тіл. В залежності від положення опори під балкою важіль може призводити до виграшу або в силі, або в переміщенні вантажів. Слід сказати, що важіль не призводить до скорочення роботи як фізичної величини, він лише дозволяє перерозподілити її виконання зручним чином.
Систему важелів з давніх пір використовує людина. Так, існують свідоцтва, що її використовували стародавні єгиптяни при будівництві пірамід. Перше математичне опис ефекту важеля відноситься до III століття до нашої ери і належить воно Архімеду. Сучасне пояснення принципу роботи цього механізму із залученням поняття моменту сили виникло лише у XVII столітті, у часи становлення класичної механіки Ньютона.
Правило важеля
За яким принципом працює важіль? Відповідь на це питання міститься в понятті про момент сили. Останнім називають таку величину, яка виходить в результаті множення плеча сили на її модуль, тобто:
M = F*d
Плече сили d являє собою відстань від точки опори до точки прикладання сили F.
Коли важіль виконує свою роботу, то на нього діють три різні сили:
- зовнішня сила, прикладена, наприклад, людиною;
- вага вантажу, який людина прагне перемістити за допомогою важеля;
- реакція опори, що діє з боку опори на балку важеля.
Реакція опори врівноважує дві інші сили, тому важіль не здійснює поступального руху в просторі. Щоб він не робив ще і обертальний рух, необхідно, щоб сума всіх моментів сил виявилася рівною нулю. Момент сили завжди відраховується щодо деякої осі. В даному випадку цією віссю є точка опори. При такому виборі осі плече дії сили реакції опори буде дорівнює нулю, тобто ця сила створює нульовий момент. На малюнку нижче показаний типовий важіль першого роду. Стрілками відзначені зовнішня сила F і вага вантажу R.
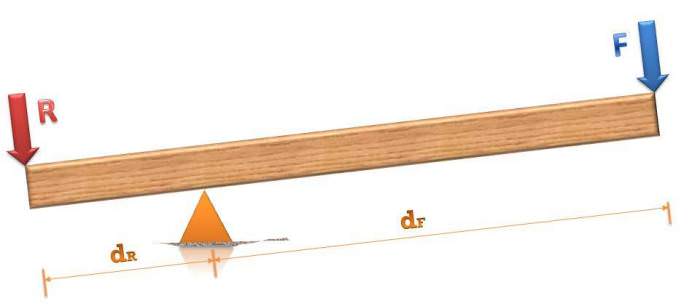
Записуємо суму моментів для цих сил, маємо:
R*dR + (-F*dF) = 0
Рівність нулю суми моментів забезпечує відсутність обертання плечей важеля. Момент сили F взято з від’ємним знаком тому, що ця сила прагне повернути важіль за годинниковою стрілкою, сила R прагне здійснити цей поворот проти годинникової стрілки.
Переписуючи це вираження в таких формах, отримаємо умови рівноваги важеля:
R*dR = F*dF;
dR/dF = F/R
Ми отримали записані рівності, використовуючи концепцію моменту сили. У III столітті до н. е. грецькі філософи не знали про цю фізичної концепції, тим не менш Архімед встановив зворотну залежність відносини діючих на плечі важеля сил від довжини цих плечей в результаті експериментальних спостережень.
Записані рівності говорять про те, що зменшення довжини плеча dR сприяє появі можливості з допомогою невеликої сили F і довгого плеча dF піднімати великі ваги R вантажів.
Що таке блок у фізиці?
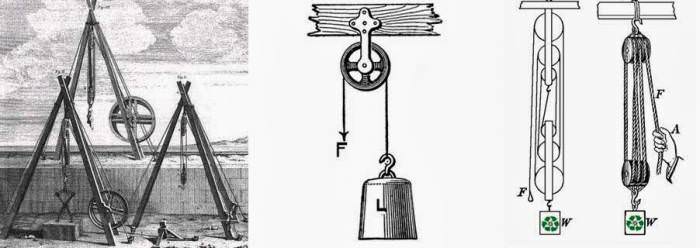
Блок – це ще один простий механізм, який являє собою круглий циліндр, що має борозну по периметру циліндричної поверхні. Борозна служить для закріплення мотузки або ланцюга. Блок має вісь обертання. На малюнку показаний приклад блоку, демонструє принцип його роботи.
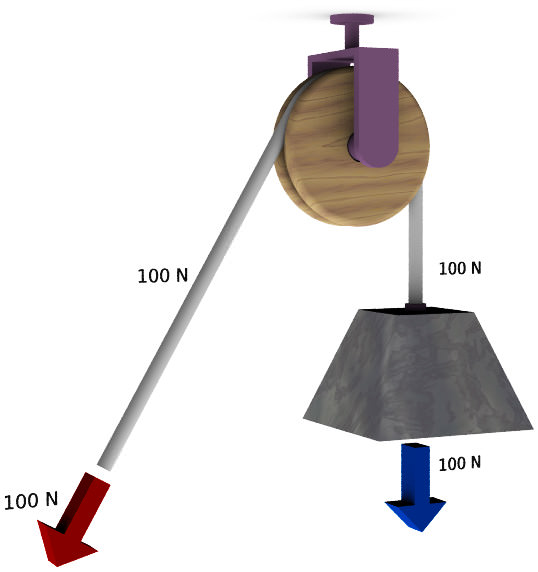
Цей блок називається нерухомим. Він не дає виграшу в силі, однак дозволяє змінити її напрямок.
Крім нерухомого, існує рухливий блок. Система з рухомого і нерухомого блоків показана нижче.
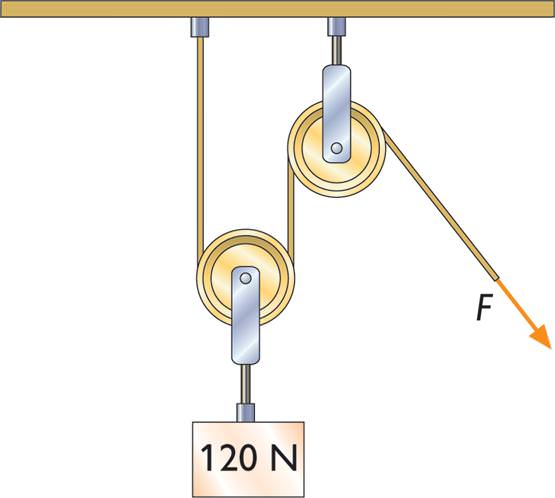
Якщо правило моментів застосувати до цієї системи, то ми отримаємо виграш у силі в два рази, але при цьому у стільки ж разів програємо у дорозі (на малюнку F = 60 Н).
Система важелів і блоків
Як вже згадувалося в попередніх пунктах, важіль може застосовуватися для виграшу в дорозі або силі, блок дозволяє виграти в силі і змінити напрямок її дії. Ці властивості розглянутих простих механізмів застосовуються в системах важелів і блоків. У цих системах кожен елемент приймає деяке зусилля і передає його іншим елементам так, що на виході ми отримуємо початкове зусилля.
Простота роботи важеля і блоку і гнучкість їх конструкційного використання дозволяють з такої сукупності складати складні механізми.
Приклади використання систем простих механізмів
По суті, будь-які машини, які нас оточують, являють собою системи важелів і блоків. Наведемо найбільш відомі приклади:
- друкарська машинка;
- піаніно;
- вантажопідіймальний кран;
- розкладні будівельні ліси;
- регульовані ліжка і столи;
- сукупність кісток, суглобів і м’язів людини.
Якщо відомо вхідна зусилля в кожній з цих систем, то вихідна сила може бути розрахована за допомогою послідовного застосування правила важеля до кожного елемента системи.