Стереометрія, як розділ геометрії в просторі, вивчає властивості призм, циліндрів, конусів, куль, пірамід і інших об’ємних фігур. Дана стаття присвячена детальному розгляду характеристик і властивостей правильної шестикутної піраміди.
Яка піраміда вивчатиметься
Правильна шестикутна піраміда являє собою фігуру в просторі, яка обмежена одним рівностороннім і рівнокутним шестикутником, і шістьма однаковими трикутниками равнобедренными. Ці трикутники можуть бути також рівносторонніми при певних умовах. Ця піраміда нижче показана.
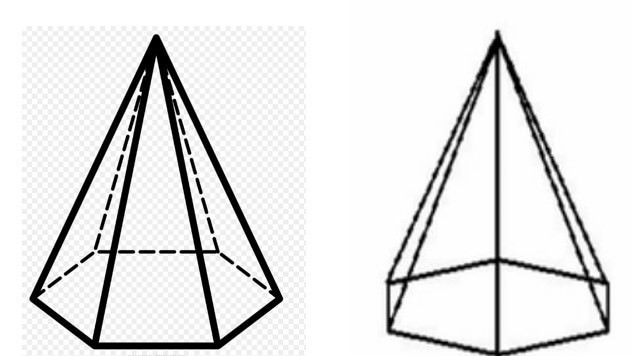
Тут зображена одна і та ж фігура, тільки в одному випадку вона повернена бічною гранню до читача, а в іншому – бічним ребром.
Правильна шестикутна піраміда має 7 граней, які були названі вище. Також їй належать 7 вершин і 12 ребер. На відміну від призм, у всіх пірамід є одна особлива вершина, яка утворена перетинанням бічних трикутників. Для правильної піраміди вона відіграє важливу роль, оскільки опущений з неї на підставу фігури перпендикуляр є заввишки. Далі висоту будемо позначати буквою h.
Показана піраміда називається правильною по двох причинах:
- в її основі знаходиться шестикутник з однаковими довжинами сторін a і з однаковими кутами 120 o;
- висота піраміди h перетинає шестикутник точно в його центрі (точка перетину лежить на однаковій відстані від усіх боків і від усіх вершин шестикутника).