Обсяг є характеристикою будь-якої фігури, яка має ненульові розміри у всіх трьох вимірах простору. У цій статті з точки зору стереометрії (геометрії просторових фігур) ми розглянемо призму і покажемо, як знаходити обсяги призм різного виду.
Що таке призма?
Стереометрія має точним відповіддю на це питання. Під призмою в ній розуміють фігуру, утворену двома багатокутними однаковими гранями і кількома параллелограммами. На малюнку нижче показано чотири різні призми.
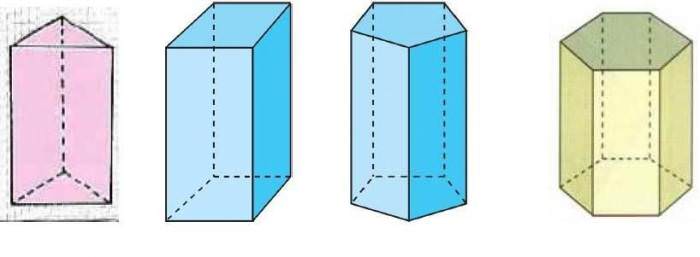
Кожну з них можна отримати наступним чином: необхідно взяти многокутник (трикутник, чотирикутник і так далі) і відрізок певної довжини. Потім кожну вершину многокутника слід перемістити за допомогою паралельних відрізків в іншу площину. У новій площині, яка буде паралельна вихідної, вийде новий багатокутник, аналогічний обраному спочатку.
Призми можуть мати різний тип. Так, вони можуть бути прямими, похилими і правильними. Якщо бічне ребро призми (відрізок, що з’єднує вершини підстав) перпендикулярно підстав фігури, то остання є прямою. Відповідно, якщо ця умова не виконується, то мова йде про похилій призми. Правильна фігура – це пряма призма з рівнокутним і рівностороннім підставою.
Далі в статті ми покажемо, як розраховувати об’єм призми кожного з названих типів.
Обсяг правильних призм
Почнемо з самого простого випадку. Наведемо формулу об’єму призми правильною, має n-вугільне основу. Формула об’єму V для будь-якої фігури розглянутого класу має наступний вигляд:
V = So*h.
Тобто для визначення обсягу достатньо розрахувати площу однієї з підстав So і помножити її на висоту h фігури.
У разі правильної призми позначимо довжину сторони її основи буквою a, а висоту, яка дорівнює довжині бічного ребра, буквою h. Якщо основа n-кутник правильний представляє, то для розрахунку його площі найпростіше скористатися такою універсальною формулою:
Sn = n/4*a2*ctg(pi/n).
Підставляючи в рівність значення числа сторін n і довжину однієї сторони a, можна обчислити площу n-вугільного підстави. Зазначимо, що функція котангенса тут обчислюється для кута pi/n, який виражений в радіанах.
Враховуючи записане для Sn рівність, отримуємо кінцеву формулу об’єму призми правильною:
Vn = n/4*a2*h*ctg(pi/n).
Для кожного конкретного випадку можна записати відповідні формули для V, але всі вони однозначно випливають із записаного загального виразу. Наприклад, для чотирикутної призми правильною, яка у загальному випадку є прямокутним параллелепипедом, отримуємо:
V4 = 4/4*a2*h*ctg(pi/4) = a2*h.
Якщо в цьому виразі прийняти h=a, то ми одержуємо формулу для об’єму куба.
Обсяг прямих призм
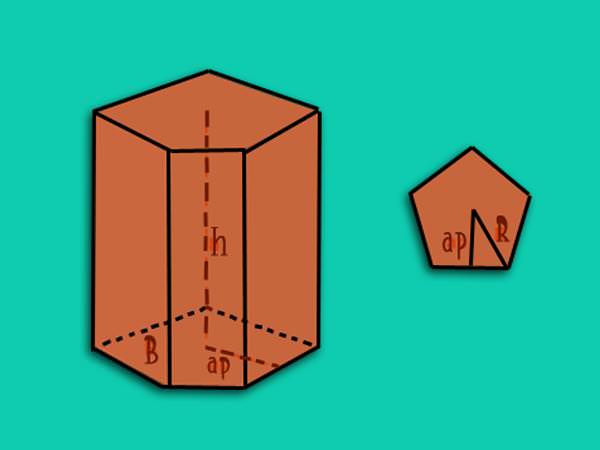
Відзначимо відразу, що для прямих фігур не існує загальної формули для обчислення об’єму, яка була наведена вище для правильних призм. При знаходженні розглянутої величини слід використовувати вихідне вираз:
V = So*h.
Тут h – це довжина бічного ребра, як і в попередньому випадку. Що стосується площі підстави So, то вона може приймати самі різні значення. Завдання розрахунку у прямої призми обсягу зводиться до знаходження площі її основи.
Розрахунок величини So слід проводити, виходячи з особливостей самого заснування. Наприклад, якщо воно є трикутником, тоді площа можна обчислити так:
So3 = 1/2*a*ha.
Тут ha – апофема трикутника, тобто його висота, опущена на основу a.
Якщо підставою є чотирикутник, то він може бути трапецією, паралелограмом, прямокутником або мати абсолютно довільний тип. Для всіх названих випадків слід скористатися відповідною формулою планіметрії для визначення площі. Наприклад, для трапеції ця формула має вигляд:
So4 = 1/2*(a1 + a2)*ha.
Де ha – висота трапеції, a1 і a2 – це її довжини паралельних сторін.
Щоб визначити площу для багатокутників більш високого порядку, слід розбивати їх на прості фігури (трикутники, чотирикутники) і розраховувати суму площ останніх.
Обсяг похилих призм
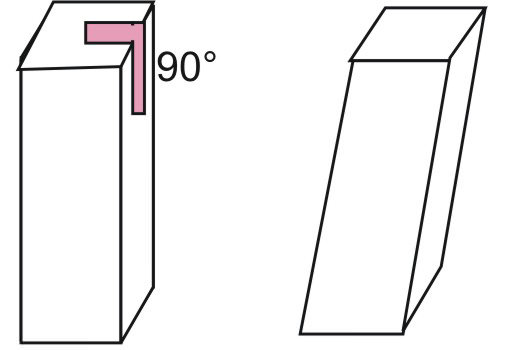
Це найскладніший випадок розрахунку об’єму призми. Загальна формула для таких фігур також застосовна:
V = So*h.
Тим не менш, до складності знаходження площі підстави, що представляє багатокутник довільного типу, додається проблема визначення висоти фігури. Вона в похилій призми завжди менше довжини бічного ребра.
Найпростіше цю висоту знайти, якщо відомий який-небудь кут фігури (плоский або двогранний). Якщо такий кут дан, тоді слід з його використанням побудувати всередині призми прямокутний трикутник, який би містив в якості однієї зі сторін висоту h і, користуючись тригонометричними функціями і теоремою Піфагора, знайти величину h.
Геометрична задача на визначення обсягу
Дана правильна призма з трикутним підставою, що має висоту 14 см і довжину сторони 5 див. Чому дорівнює об’єм трикутної призми?

Оскільки мова йде про правильну фігуру, то ми вправі скористатися відомою формулою. Маємо:
V3 = 3/4*a2*h*ctg(pi/3) = 3/4*52*14*1/√3 = √3/4*25*14 = 151,55 см3.
Трикутна призма є досить симетричною фігурою, у формі якої часто виконують різні архітектурні споруди. Цю призму зі скла використовують в оптиці.












