Лямбда-числення — це формальна система в математичній логіці для вираження підрахунків на основі абстракції і застосування функцій з використанням прив’язки і заміни змінних. Це універсальна модель, яку можна застосовувати для проектування будь-якої машини Тюрінга. Вперше введена лямбда-числення Черчем, відомим математиком, у 1930-х роках.
Система складається з побудови лямбда-членів і виконання над ними операцій скорочення.
Пояснення і додатки
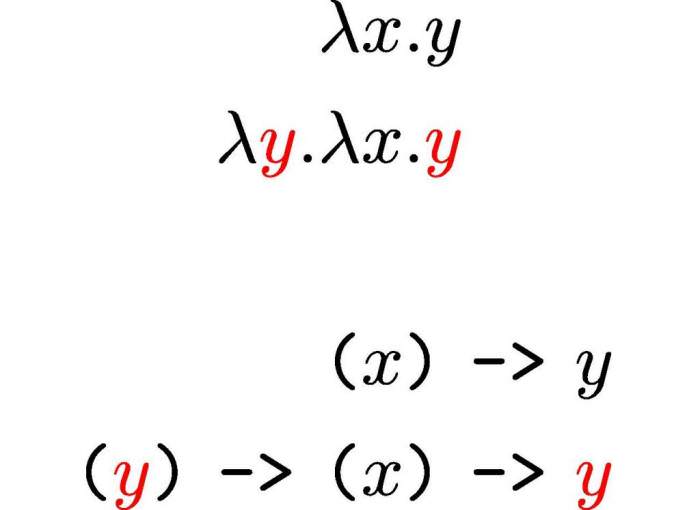
Грецька буква lambda (λ) використовується в лямбда-вирази та лямбда-терміни для позначення зв’язування змінної функції.
Лямбда-числення може бути нетипизировано або надруковане. У першому варіанті функції можуть бути застосовані лише в тому випадку, якщо вони здатні приймати дані цього типу. Типізовані лямбда-числення слабкіше, можуть виражати менше значення. Але, з іншого боку, вони дозволяють доводити більше речей.
Однією з причин того, що існує багато різних типів — це бажання вчених зробити більше, не відмовляючись від можливості доводити сильні теореми лямбда-числення.
Система знаходить застосування в багатьох областях математики, філософії, лінгвістики, і комп’ютерних наук. В першу чергу, лямбда-числення — це розрахунок, який зіграв важливу роль у розвитку теорії мов програмування. Саме стилі функціонального створення реалізують системи. Вони також є актуальною темою досліджень в теорії цих категорій.