Стереометрія є важливою частиною загального курсу геометрії, яка розглядає характеристики просторових фігур. Однією з таких постатей є чотирикутна призма. У цій статті детальніше розкриємо питання, як розраховувати обсяг чотирикутної призми.
Що собою являє чотирикутна призма?
Очевидно, що перш ніж наводити формулу обсягу чотирикутної призми, необхідно дати чітке визначення цієї геометричної фігури. Під такою призмою розуміють тривимірний многогранник, який обмежений двома довільними однаковими чотирикутниками, що лежать у паралельних площинах, і чотирма параллелограммами.
Зазначені паралельні один одному чотирикутники називаються підставами фігури, а чотири паралелограма – це бічні сторони. Тут слід пояснити, що паралелограми також є чотирикутниками, однак підстави не завжди є параллелограммами. Приклад неправильного чотирикутника, який цілком може бути підставою призми, показаний нижче на малюнку.
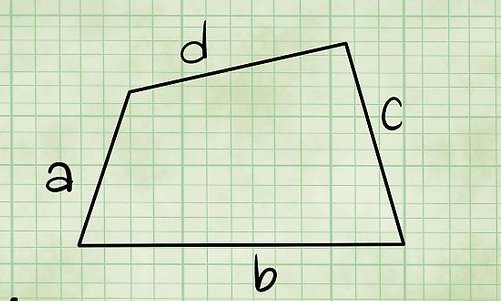
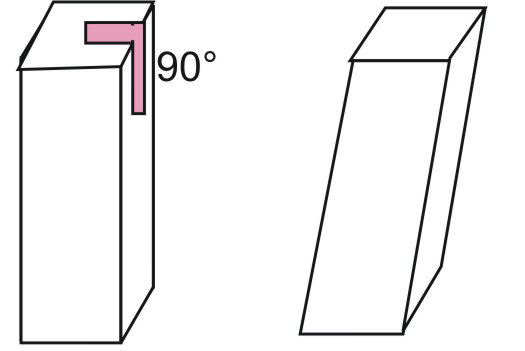
Будь-чотирикутна призма складається з 6 сторін, 8 вершин і 12 ребер. Існують чотирикутні призми різних видів. Наприклад, фігура може бути похилій або прямий, неправильної і правильною. Далі в статті покажемо, як можна розраховувати обсяг чотирикутної призми з урахуванням її виду.