Вивчаючи поведінку газів у фізиці, часто виникають задачі на визначення запасеної в них енергії, яку теоретично можна використовувати для здійснення деякої корисної роботи. У цій статті розглянемо питання, за якими формулами внутрішня енергія ідеального газу може бути розрахована.
Поняття про ідеальному газі

Чітке розуміння концепції ідеального газу важливо при вирішенні завдань з системами, що знаходяться в цьому агрегатному стані. Будь газ приймає форму і об’єм посудини, в який його поміщають, проте, не всякий газ є ідеальним. Наприклад, повітря можна вважати сумішшю ідеальних газів, в той же час водяна пара не є таким. В чому ж полягає принципова різниця між реальними газами та їх ідеальною моделлю?
Відповіддю на поставлене питання будуть дві такі особливості:
- співвідношення між кінетичною і потенційною енергією молекул і атомів, що складають газ;
- співвідношення між лінійними розмірами частинок газу і середньою відстанню між ними.
Газ вважається ідеальним тільки в тому випадку, коли середня кінетична енергія його часток набагато більше енергії зв’язку між ними. Різниця між цими енергіями така, що можна вважати, що взаємодія між частинками повністю відсутня. Також для ідеального газу характерна відсутність розмірів у його частинок, вірніше ці розміри можна не враховувати, оскільки вони набагато менше середніх межчастичных відстаней.
Хорошими емпіричними критеріями, що дозволяють визначити ідеальність газової системи, є такі її термодинамічні характеристики, як температура і тиск. Якщо перша більше 300 К, і друге менше 1 атмосфери, то будь газ може покладатися ідеальним.
Що це внутрішня енергія газу?
Перш ніж записати формулу внутрішньої енергії ідеального газу, необхідно познайомитися з цією характеристикою ближче.
В термодинаміці внутрішню енергію, як правило, позначають латинською буквою U. Визначається в загальному випадку вона за наступною формулою:
U = H – P*V
Де H – ентальпія системи, P і V – тиск і об’єм.
За своїм фізичним змістом внутрішня енергія складається з двох складових: кінетичної і потенційної. Перша пов’язана з різного роду рухом частинок системи, а друга – з силовим взаємодією між ними. Якщо застосувати це визначення до концепції ідеального газу, у якого відсутня потенційна енергія, то величина U при будь-якому стані системи буде точно дорівнює його кінетичній енергії, тобто:
U = Ek.
Висновок формули внутрішньої енергії
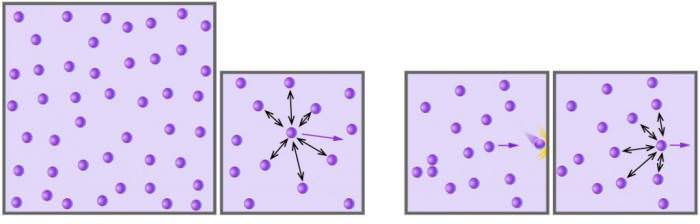
Вище ми встановили, що для її визначення у системи з ідеальним газом необхідно розрахувати його кінетичну енергію. З курсу загальної фізики відомо, що енергія частинки масою m, яка поступально рухається в певному напрямку зі швидкістю v, визначається за формулою:
Ek1 = m*v2/2.
Її також можна застосувати для газових частинок (атомів і молекул), однак, необхідно зробити деякі зауваження.
По-перше, під швидкістю v слід розуміти деяку середню величину. Справа в тому, що газові частинки рухаються з різними швидкостями відповідно до розподілу Максвелла-Больцмана. Останнє дозволяє визначити середню швидкість, яка з плином часу не змінюється, якщо відсутні зовнішні впливи на систему.
По-друге, формула для Ek1 передбачає енергію на одну ступінь свободи. Газові частинки можуть рухатися у всіх трьох напрямках, а також обертатися в залежності від їх будови. Щоб врахувати величину ступеня свободи z, її слід помножити на Ek1, тобто:
Ek1z = z/2*m*v2.
Кінетична енергія всієї системи Ek в N разів більше, ніж Ek1z, де N – загальна кількість газових частинок. Тоді для U отримуємо:
U = z/2*N*m*v2.
Згідно цій формулі, зміна внутрішньої енергії газу можливо тільки в тому випадку, якщо поміняти число частинок N в системі, або їх середню швидкість v.
Внутрішня енергія і температура
Застосовуючи положення молекулярно-кінетичної теорії ідеального газу, можна отримати наступну формулу зв’язку між середньою кінетичною енергією однієї частинки і абсолютною температурою:
m*v2/2 = 1/2*kB*T.
Тут kB – стала Больцмана. Підставляючи це рівність у формулу для U, отриману в пункті вище, приходимо до наступного виразу:
U = z/2*N*kB*T.
Цей вираз можна переписати через кількість речовини n і газову сталу R в наступному вигляді:
U = z/2*n*R *T.
Згідно з цією формулою, зміна внутрішньої енергії газу можливо, якщо змінити його температуру. Величини U і T залежать один від одного лінійно, тобто графік функції U(T) являє собою пряму лінію.
Як будову газової частинки впливає на внутрішню енергію системи?
Під будовою частинки газу (молекули) мається на увазі кількість атомів, яка її складає. Воно відіграє визначальну роль при підстановці відповідного ступеня свободи z у формулу для U. Якщо газ є одноатомным, формула внутрішньої енергії газу приймає такий вигляд:
U = 3/2*n*R*T.
Звідки взялася величина z=3? Її поява пов’язана лише з трьома ступенями свободи, якими володіє атом, оскільки він може рухатися тільки в одному з трьох просторових напрямків.
Якщо розглядається двухатомная молекула газу, внутрішню енергію слід обчислювати за такою формулою:
U = 5/2*n*R*T.
Як бачимо, двухатомная молекула вже має 5 ступенів свободи, 3 з яких є поступальними і 2 обертальними (згідно з геометрії молекули, вона може обертатися навколо двох взаємно перпендикулярних осей).
Нарешті, якщо газ є трьох – і більше атомним, то справедливо наступне вираз для U:
U = 3*n*R*T.
Складні молекули мають 3 поступальних і 3 обертальних ступенів свободи.
Приклад завдання
Під поршнем знаходиться одноатомний газ при тиску 1 атмосфера. В результаті нагрівання газ розширився так, що його обсяг збільшився від 2-х літрів до 3-х. Як при цьому змінилася внутрішня енергія газової системи, якщо процес розширення був изобарным.
Щоб вирішити цю задачу, недостатньо наведених у статті формул. Необхідно згадати про рівняння стану ідеального газу. Воно має вигляд, представлений нижче.
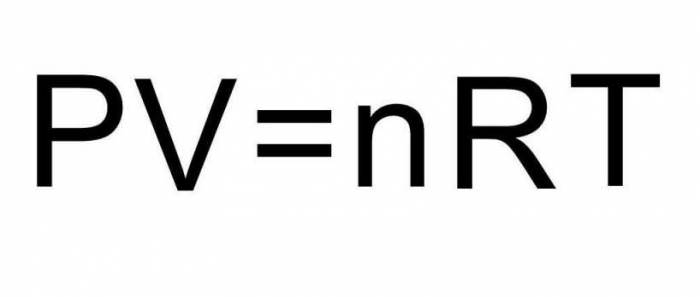
Оскільки поршень закриває циліндр з газом, то в процесі розширення кількість речовини n залишається постійним. Під час изобарного процесу температура змінюється прямо пропорційно обсягу системи (закон Шарля). Це означає, що вище формула запишеться так:
P*ΔV = n*R*T.
Тоді вираз для внутрішньої енергії одноатомного газу прийме форму:
ΔU = 3/2*P*ΔV.
Підставляючи в це рівняння значення тиску і зміни обсягу в одиницях СІ, отримуємо відповідь: ΔU ≈ 152 Дж.