Кількість руху, яке часто називають імпульсом тіла, є ключовою фізичною величиною в ньютонівській механіці. Наведемо в даній статті формулу імпульсу, пояснимо її значення, а також розглянемо інші величини і закони, пов’язані з нею.
Імпульс тіла і другий закон Ньютона
На початку XVII століття Галілео Галілей, вивчаючи закони механічного руху тіл, ввів у фізику важливу величину, яку він назвав кількістю руху. Згодом Ісаак Ньютон використовував досягнення італійського вченого при формулюванні своїх законів. Обидва вчених під кількістю руху розуміли твір інерційної маси тіла на лінійну швидкість його переміщення у просторі, тобто:
p = m*v.
Величина p є векторною, яка спрямована точно так само, як швидкість v. Фізичний сенс кількості руху полягає в прояві інерційних властивостей тіла і його кінетичної енергії одночасно.
Якщо взяти похідну по часу від p, то ми отримаємо другий ньютонівський закон:
dp/dt = m*dv/dt = m*a = F.
Це рівність можна переписати в наступному вигляді:
dp = F*dt.
Це вислів говорить про те, що чинна протягом часу dt сила F призводить до зміни кількості руху на величину dp. В правій частині рівності варто величина, яку називають імпульсом сили. З цієї причини вираз для кількості руху p стали називати формулою імпульсу.
Збереження імпульсу
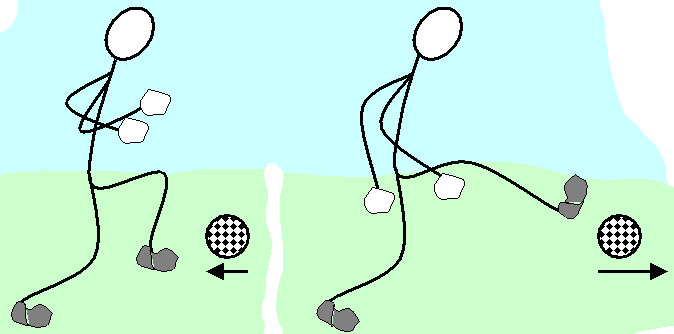
Важливість досліджуваної величини полягає в тому, що вона зберігає своє значення в закритих системах. Це означає, що якщо на тіла системи діють лише внутрішні сили, то кількість руху між ними розподіляється в результаті внутрішніх взаємодій, повний же імпульс не змінюється з плином часу, тобто:
p = const, якщо F = 0.
Типовими видами взаємодії є зіткнення тіл, наприклад, куль. Зіткнення можуть бути абсолютно пружними, абсолютно пластичними або носити проміжний характер. Проте незалежно від типу зіткнення, сумарний імпульс завжди зберігається, що не можна сказати про кінетичної енергії. Вона зберігається лише у випадку пружних зіткнень. При будь-якому іншому типі взаємодії частина її витрачається на нагрівання тіл, тобто переходить в теплову енергію.
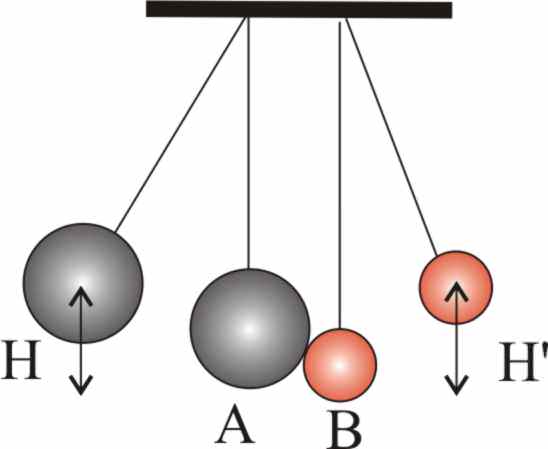
Коли вирішують завдання, то формулою збереження імпульсу слід користуватися по компонентно, тобто в процесі внутрішніх взаємодій тіл кожен компонент сумарного імпульсу залишається незмінним.
Момент імпульсу
Якщо розглянута вище величина p характеризує лінійне переміщення тіла, то момент імпульсу L – це властивість системи обертання. Для матеріальної точки масою m, що обертається навколо осі на відстані r зі швидкістю v, формула моменту імпульсу має вигляд:
L = [r*p] = [r*m*v].
Квадратні дужки вказують на векторний добуток. Напрямок L перпендикулярно площині обертання точки і визначається за правилом правої руки.
Так само як і p, величина L зберігається, якщо відсутні зовнішні впливи на систему (момент сили дорівнює нулю). Якщо вираз вище далі перетворювати, використовуючи кутову швидкість ω і момент інерції I, то закон збереження моменту імпульсу запишеться у вигляді:
L = I*ω = const.
В дії цей закон можна спостерігати, коли фігурист обертається на льоду, групуючи різним чином своє тіло.

Приклад завдання з кулями
Використовуючи формулу імпульсу, знаючи про закон його збереження, розв’яжемо таку задачу. Припустимо, що дві кулі однакової маси m летять один на одного. Швидкість першої кулі становить v1, другого – v2. Необхідно визначити швидкість куль після зіткнення, знаючи, що v1 = 2*v2. Удар можна вважати абсолютно непружним.
Після зіткнення два кулі будуть рухатися як єдине тіло, тому справедлива наступна формула імпульсу:
m*v1 – m*v2 = 2*m*u.
За позитивний напрямок швидкості обрано напрямок польоту першого кулі. Висловлюючи звідси u, і підставляючи рівність v1 = 2*v2, отримуємо:
u = 1/2*(v1 – v2) = v2/2.
Таким чином, після зіткнення два тіла будуть рухатися в бік руху першого тіла зі швидкістю v2/2.