Початок всьому поклали греки. Не нинішні, а ті, що жили раніше. Калькуляторів ще не було, а потреби в обчисленнях вже присутні. І майже будь обчислення призводило зрештою до прямокутних трикутниках. Вони дали рішення багатьох проблем, одна з яких звучала так: “Як знайти гіпотенузу, знаючи кут і катет?”.
Трикутники з прямим кутом
Незважаючи на простоту визначення, ця фігура на площині може задати чимало загадок. Багато випробували це на собі, хоча б у шкільній програмі. Добре ще, що на всі запитання він сам дає відповіді.
Але не можна ще спростити це нескладне поєднання сторін і кутів? Виявилося, можна. Досить зробити один кут прямий, тобто рівним 90°.
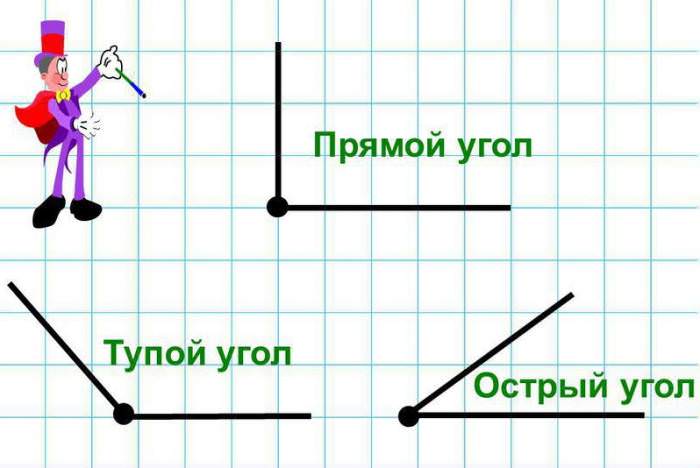
Здавалося б, яка різниця? Величезна. Якщо у всьому різноманітті кутів розібратися майже неможливо, то, зафіксувавши один з них, легко прийти до дивних висновків. Що і зробив Піфагор.
Він придумав слова “катет” і “гіпотенуза” або це зробив хтось інший — неважливо. Головне, що вони отримали імена не просто так, а завдяки своїм стосункам з прямим кутом. Дві сторони прилягали до нього. Це і були катети. Третя противолежала, вона стала гіпотенузою.