Кожному школяреві відомо, що при наявності контакту між двома твердими поверхнями виникає так звана сила тертя. Розглянемо в цій статті, що вона собою являє, концентруючи свою увагу на точці прикладання сили тертя.
Яких видів буває сила тертя?
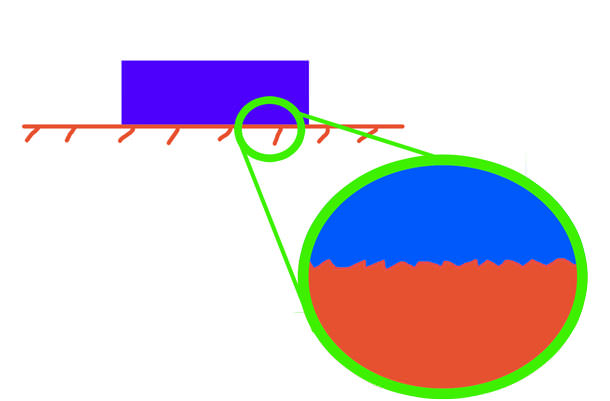
Перш ніж розглядати точку прикладання сили тертя, необхідно коротко згадати, які види тертя існують в природі і техніці.
Почнемо розглядати тертя спокою. Цей вид характеризує стан спочиваючого твердого тіла на якій-небудь поверхні. Тертя спокою перешкоджає будь-зміщення тіла з його стану спокою. Наприклад, внаслідок дії цієї самої сили нам важко зрушити шафа, що стоїть на підлозі.
Тертя ковзання — це ще один вид тертя. Він проявляє себе у випадку контакту між двома ковзними один по одному поверхнями. Тертя ковзання перешкоджає руху (напрям сили тертя протилежно швидкості тіла). Яскравим прикладом його дії є ковзання по снігу лижника або ковзаняра по льоду.
Нарешті, третій вид тертя — це кочення. Він існує завжди, коли одне тіло котиться по поверхні іншого. Наприклад, кочення колеса або підшипників — це яскраві приклади, коли важливо враховувати силу тертя кочення.
Перші два з наведених видів виникають із-за нерівностей на поверхнях, що труться. Третій вид виникає через деформаційного гістерезису котиться тіла.
Точки прикладання сил тертя ковзання і спокою
Вище було сказано, що тертя спокою перешкоджає діючої зовнішньої сили, яка прагне зрушити з місця об’єкт вздовж поверхні контакту. Це означає, що напрям сили тертя протилежно напрямку паралельною до поверхні зовнішньої сили. Точка докладання розглянутої сили тертя в області контакту двох поверхонь.
Важливо розуміти, що сила тертя спокою не є величиною постійною. Вона має максимальне значення, яке розраховується за такою формулою:
Ft = ut*N.
Однак це максимальне значення з’являється тільки тоді, коли тіло починає свій рух. В будь-якому іншому випадку сила тертя спокою по модулю точно дорівнює паралельній поверхні зовнішньої сили.
Що стосується точки прикладання сили тертя ковзання, то вона не відрізняється від такої для тертя спокою. Кажучи про різницю між тертям спокою і ковзання, слід зазначити абсолютне значення цих сил. Так, сила тертя ковзання для даної пари матеріалів є постійною величиною. Крім того, вона завжди менше максимальної сили тертя спокою.
Як можна помітити, точка прикладання сил тертя не збігається з центром ваги тіла. Це означає, що ці сили створюють момент, який прагне перекинути ковзне тіло вперед. Останнє можна спостерігати, коли велосипедист різко гальмує переднім колесом.

Тертя кочення і її точка докладання
Оскільки фізична причина появи тертя кочення відрізняється від такої для розглянутих вище видів тертя, то точка прикладання сили тертя кочення має дещо інший характер.
Припустимо, що колесо автомобіля стоїть на асфальті. Очевидно, що це колесо деформується. Площа зіткнення його з асфальтом дорівнює 2*d*l, де l – ширина колеса, 2*d – довжина бічного контакту колеса і асфальту. Сила тертя кочення по своїй фізичній суті проявляється у вигляді моменту реакції опори, спрямованого проти обертання колеса. Цей момент розраховується так:
M = N*d
Якщо його розділити і помножити на радіус колеса R, тоді отримаємо:
M = N*d/R*R = Ft*R, де Ft = N*d/R
Таким чином, сила тертя кочення Ft насправді є реакцією опори, що створює момент сили, який прагне уповільнити обертання колеса.
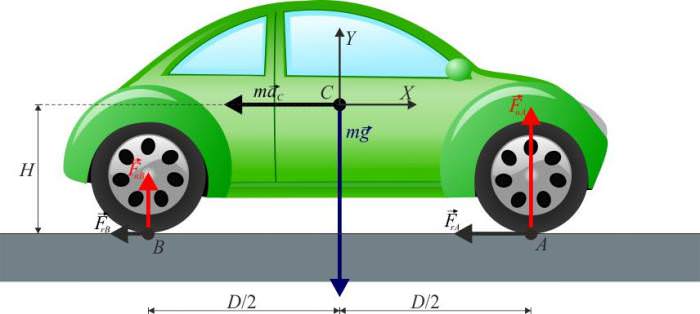
Точка прикладання цієї сили спрямована вертикально вгору відносно поверхні площини і зміщена вправо від центру мас на величину d (за умови, що колесо рухається зліва направо).
Приклад розв’язання задачі
Дія тертя сили будь-якого виду прагне сповільнити механічний рух тіл, переводячи при цьому їх кінетичну енергію в теплову. Розв’яжемо наступну задачу:
- брусок ковзає по похилій поверхні. Необхідно розрахувати прискорення його руху, якщо відомо, що коефіцієнт для ковзання дорівнює 0,35, а кут нахилу поверхні дорівнює 35o.
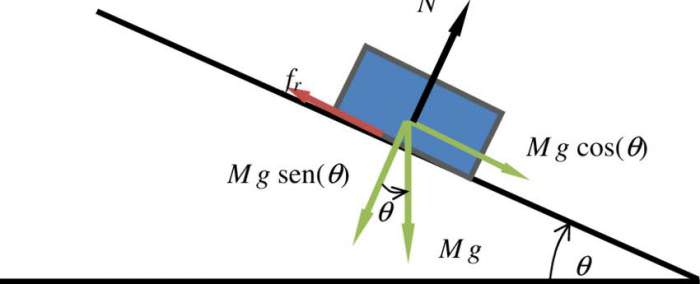
Розглянемо, які сили на брусок діють. По-перше, вниз уздовж поверхні ковзання спрямована сили тяжіння складова. Вона дорівнює:
F = m*g*sin(α)
По-друге, вгору вздовж по площині діє постійна сила тертя, яка спрямована проти вектора прискорення тіла. Її можна визначити за формулою:
Ft = ut*N = ut*m*g*cos(α)
Тоді закон Ньютона для рухається з прискоренням a бруска прийме вигляд:
m*a = m*g*sin(α) – ut*m*g*cos(α) =>
a = g*sin(α) – ut*g*cos(α)
Підставляючи в рівність дані, отримуємо, що a = 2,81 м/с2. Зауважимо, що знайдене прискорення не залежить від маси бруска.












