Одним з важливих многогранників, властивості якого детально вивчають у стереометрії, є призма. У статті розглянемо цю фігуру, розкриваючи докладніше питання, що це – правильна призма. Також наведемо формули, які дозволяють обчислити її обсяг і площа.
Фігура призма
Призма – це геометрична фігура, яка складається з n + 2 граней, де n – кількість сторін плоского многокутника. Дві грані призми є абсолютно однаковими багатокутниками. Вони розташовані в паралельних площинах і називаються підставами. Сторони підстав з’єднуються між собою параллелограммами. Цих паралелограмів n штук, всі вони утворюють бічну поверхню просторової фігури.
Крім граней, призма має вершини (2 × n) і ребра (3 × n). Вершини все є однотипними, а ось ребра бувають двох видів: що відносяться до підстав і до бічних сторін.
Будь-яку призму можна отримати, якщо паралельно самому собі перенести багатокутник з однієї площини в іншу в просторі. Нижче показаний приклад шестикутної призми, що має два шестикутних правильних підстави. Як можна бачити з рисунку, її бічна поверхня утворена шістьма прямокутниками (приватний випадок паралелограмів). Така фігура є правильною призмою. Розглянемо детальніше її в статті.
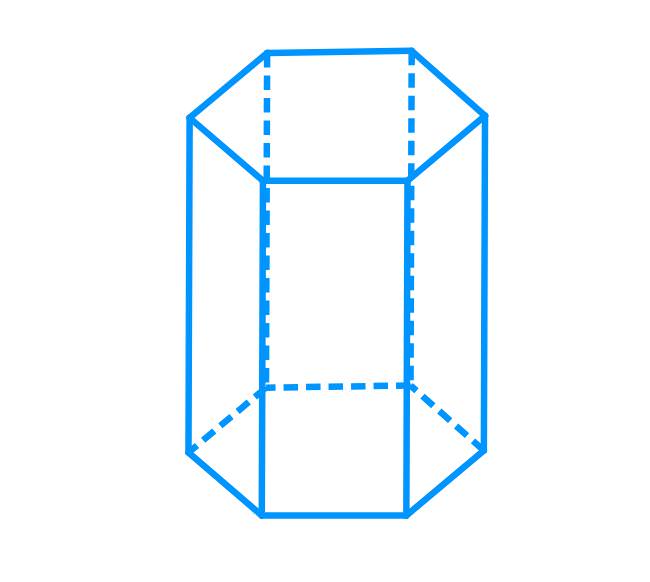
Що це – правильна призма?
Існує кілька різних класифікацій призм. Так, бувають фігури прямі або похилі, опуклі і увігнуті, п’ятикутні і десятиугольные, але сама симетрична серед усіх досліджуваних фігур – це правильна призма. Під нею вважають таку фігуру, яка має правильне підставу і є прямою. Розберемо по порядку кожен пункт цього визначення.
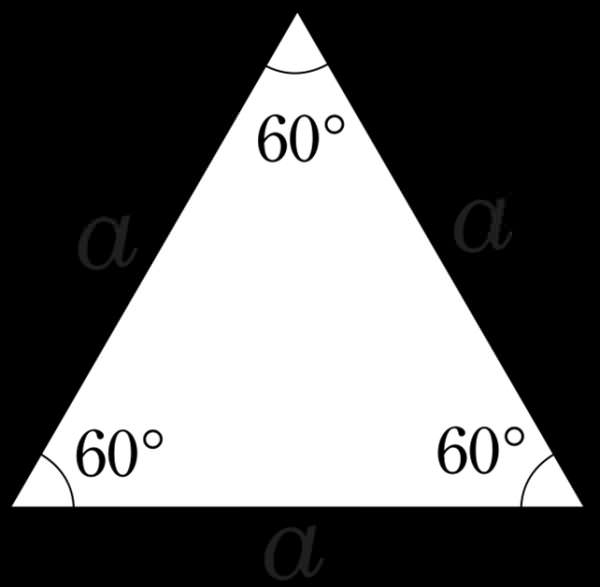
Під правильним підставою призми розуміють багатокутник, який має всі однакові сторони і всі однакові кути. Найпростішим з таких багатокутників є трикутник рівносторонній, кути якого дорівнюють 60o. Далі, збільшуючи кількість сторін, отримуємо квадрат, правильні п’ятикутник і шестикутник і так далі.
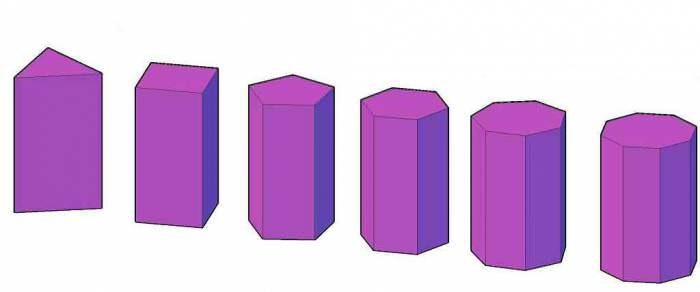
Як було сказано в ухвалі, правильна призма – пряма призма. Призмою прямої називається така фігура, у якої всі бічні паралелограми являють собою прямокутники. Більш того, ці прямокутники перпендикулярні підстав. Останній факт призводить до того, що довжина бічного ребра будь-якого з прямокутників виявляється рівною висоті фігури. На малюнку нижче показаний набір правильних призм (починаючи від трикутної і закінчуючи восьмикутної).
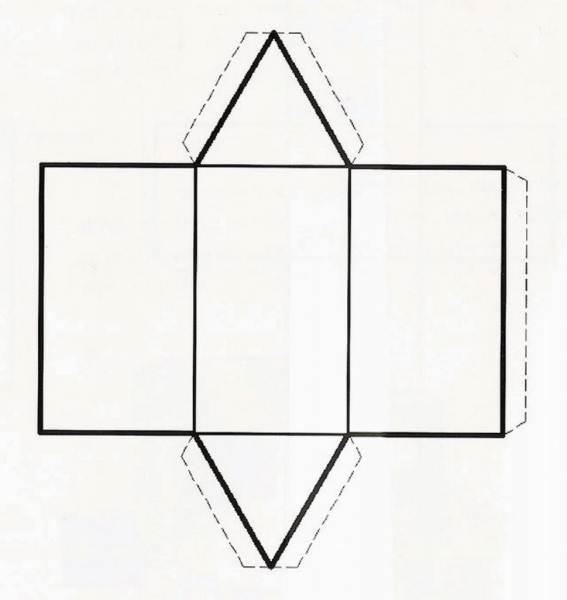
Лінійні параметри фігури
Розібравшись, що це – правильна призма, дамо характеристику параметрами, які використовуються для її опису. В першу чергу це довжина сторони її основи a і висота h. Як було зазначено, висота дорівнює довжині бічного ребра b.
Крім цих величин, також призми характеризуються діагоналями. Діагоналі бувають трьох типів: що лежать в основах, на бічних сторонах і всередині самої фігури. Розрахунок довжин діагоналей передбачає використання теореми Піфагора. Наприклад, для правильної чотирикутної призми об’ємні діагоналі дорівнюють:
d1 = √(2 × a2 + b2).
Діагоналі підстави d2 і бічних прямокутників d3 складають:
d2 = a × √2;
d3 = √(a2 + b2).
Зауважимо, що формула для діагоналей d3 буде однаковою для будь-яких багатокутних правильних призм. Що стосується обчислення діагоналей d1 і d2 для інших призм (п’ятикутні, шестикутної і так далі), то для цього слід проводити послідовні геометричні розрахунки з урахуванням властивостей відповідних правильних багатокутників.
Обчислення площі та об’єму
Площа поверхні досліджуваної фігури являє собою суму площ двох n-косинців і n прямокутників. Площа одного n-вугільного підстави можна розрахувати за наступною формулою:
Sn = n / 4 × ctg (pi / n) × a2.
Якщо позначити буквою b бічне ребро призми площа бічної поверхні складе:
Sb = n × a × b.
Тоді сумарна площа буде дорівнює:
S = n / 2 × ctg (pi / n) × a2 + n × a × b.
Перший доданок у виразі – це площа відразу двох підстав.
Обсяг призми довільного виду обчислюється так:
V = So × h
Тобто достатньо помножити на висоту h підстави площа So, щоб обчислити шукану величину. Оскільки ми знаємо як розраховувати площа підстави, то, підставляючи відповідну формулу вираз для V, приходимо до наступного результату:
V = n / 4 × ctg (pi / n) × × a2 × h.
Зазначимо, що для обчислення площі та об’єму досліджуваного виду призм достатньо знати лише два їх лінійних параметра.
Завдання з трикутною призмою
Відомо, що висота основи правильної трикутної призми дорівнює висоті об’ємної фігури і становить 11 див. Необхідно знайти для цієї призми об’єм та площу повної поверхні.
З умови задачі нам відомі два параметра, тому будь-які властивості фігури можна однозначно розрахувати. Щоб знайти довжину сторони трикутного підстави, слід згадати властивості рівностороннього трикутника. Зокрема, його висота одночасно є також бісектрисою. Це дозволяє скористатися визначенням функції косинуса, щоб довжину висоти підстави ha записати в наступному вигляді:
ha = a × cos(30o) = √3 / 2 × a.
Звідки обчислюємо a:
a = 2 × ha / √3 = 12,7 див.
Оскільки a і h відомі, то можна скористатися формулами для площі та обсягу:
S = n / 2 × ctg (pi / n) × a2 + n × a × b = √3 / 2 × 12,72 + 3 × 12,7 × 11 = 558,78 см2;
V = n / 4 × ctg (pi / n) × a2 × h = √3/4 × 12,72 × 11 = 768,25 см3.
При використанні формули S ми застосували властивість рівності висоти і бічного ребра для правильної призми.












