Рух є одним з головних властивостей світу, в якому ми живемо. З фізики відомо, що всі тіла і частинки, з яких вони складаються, постійно переміщаються в просторі навіть при абсолютному нулі температур. В даній статті розглянемо визначення прискорення як важливої кінематичної характеристики механічного руху в фізиці.
Про яку величиною йде мова?
Згідно з визначенням прискорення – це величина, що дозволяє кількісно описати процес зміни швидкості від часу. Математично прискорення обчислюється наступним чином:
a = dv/dt.
Ця формула визначення прискорення описує так звану миттєву величину a. Щоб обчислити середнє прискорення, слід взяти відношення різниці швидкостей до більш тривалого проміжку часу.
Величина a являє собою вектор. Якщо швидкість спрямована вздовж дотичної до розглянутої траєкторії переміщення тіла, то прискорення може бути направлено абсолютно довільним чином. Воно ніяк не пов’язано з траєкторією переміщення і з вектором v. Тим не менш обидві названі характеристики руху залежать від прискорення. Це відбувається тому, що в кінцевому рахунку саме вектор прискорення визначає траєкторію і швидкість тіла.
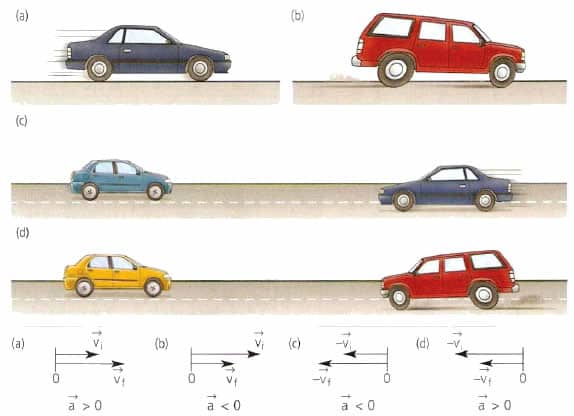
Щоб зрозуміти, куди направлено прискорення a, слід записати другий ньютонівський закон. У загальновідомій формі він виглядає так:
F = m*a.
Рівність говорить про те, що два вектори (F і a) пов’язані один з одним через числову константу (m). Властивості векторів відомо, що множення на позитивне число не змінює напрямку вектора. Іншими словами, прискорення спрямоване завжди в бік дії сумарної сили F на тіло.
Вимірюється ця величина в метрах в квадратну секунду. Наприклад, сила тяжіння Землі поблизу її поверхні повідомляє тіл прискорення 9,81 м/с2, тобто швидкість вільно падаючого тіла в безповітряному просторі за кожну секунду зростає на 9,81 м/с.