Всі види руху, з якими людина стикається протягом свого життя, вивчаються в фізиці в рамках законів класичної механіки Ньютона. У даній статті мова піде про обертання твердих тіл, про рівняннях, які його описують, і про формулах кутового прискорення.
Обертання в природі і техніці

Перш ніж вивчати кутове прискорення і формули, які дозволяють визначити, розглянемо, що являє собою процес обертання.
У фізиці під обертанням розуміють такий тип руху, при якому кожна точка тіла довільної форми або матеріальна точка рухається по круговій траєкторії. Через центр цієї траєкторією перпендикулярно до її площини, що проходить вісь обертання. Розглянутий тип переміщення в просторі може відбуватися з постійною швидкістю або з змінної. В останньому випадку говорять про наявність у прискорення тіла.
Прикладами обертання в побуті є рух лопатей вентилятора, обертання коліс велосипеда і автомобіля, обертання ножів блендера або робочої частини міксера, рух валів і шестерень. У природі можна спостерігати цей тип руху, наприклад, переміщення нашої Землі навколо Сонця і її добове обертання навколо своєї осі.
Якими величинами описують обертання?
Оскільки розглянутий вид руху відбувається по круговій траєкторії, то виявляється зручним описати його за допомогою величин, які використовують величину кута кругового сектора. Перерахуємо ці величини.
Кут θ – це центральний кут кругового сектора. Для наочності він показаний нижче на малюнку.
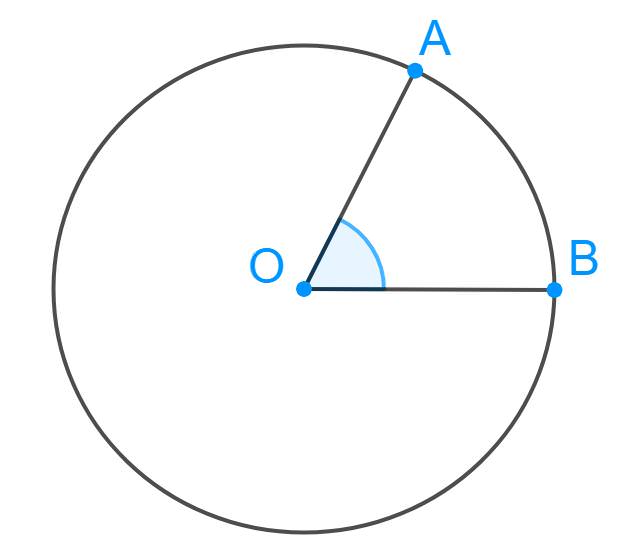
Тут дуга AB – це відстань, яку пройшло обертове тіло за деякий проміжок часу t. Використовуючи відповідну пропорцію, можна отримати зв’язок між довжиною цієї дуги L і кутом θ, виражений в радіанах. Цей зв’язок має такий математичний вигляд:
L = θ × r
Символом r позначено радіус кола. Нагадаємо, що один оберт по круговій траєкторії відповідає куту θ = 2 × pi.
Наступна важлива кінематична величина обертання – це швидкість. Її, як правило, позначають грецькою буквою ω (омега) та визначають в радіанах в секунду. Відмінність цієї швидкості, яка називається кутовий, від її лінійного аналога є очевидним, оскільки остання вимірюється в метрах за секунду. Математично величина ω визначається так:
ω = dθ / dt
Тобто кутова швидкість показує швидкість повороту тіла. Записане вираз називається миттєвою швидкістю, обчисленої нескінченно малий проміжок часу (t; t + dt). Формула для середньої швидкості ωm запишеться у вигляді:
ωm = θ / t
При цьому на кутовому проміжку θ миттєва швидкість ω може значно змінюватися.
Нарешті, третьою важливою величиною, яка використовується для опису нерівномірного руху по колу, є кутове прискорення α. Ця величина показує як змінюється швидкість на даному проміжку часу. Формула кутового прискорення через кутову швидкість виглядає наступним чином:
α = dω / dt
Звідси випливає, що одиницею вимірювання α є радіан в квадратну секунду (рад/с2).
Динаміка обертання і кутове прискорення
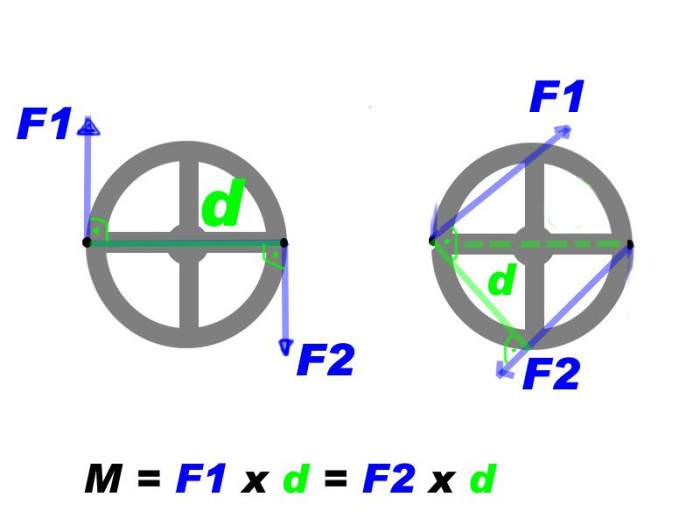
Згадуючи закони Ньютона для руху, можна сказати, що будь-яка зміна в механічному переміщенні твердого тіла пов’язане з дією деякої зовнішньої сили. У разі обертання розглядають не саму силу, а її момент. Останній дорівнює векторному добутку сили на вектор відстані від осі до точки прикладання сили, тобто:
M = [r × F]
Цей момент призводить або до гальмування обертання, або до його прискоренню. В обох випадках рівняння руху в скалярної формі записується у вигляді:
M = I × α
Де I-момент інерції (аналог маси тіла для прямолінійного руху). Остання рівність дозволяє записати формулу для обчислення кутового прискорення в динаміці:
α = M / I.
Таким чином, знаючи моменти сили інерції, можна розрахувати прискорення α.
Кінематика прискореного обертання
Якщо швидкість обертання протягом деякого часу не змінює своєї величини, то говорити про кутовому прискоренні тіла не доводиться, оскільки воно дорівнює нулю. Якщо ж швидкість змінюється з плином часу, то рух називається прискореним. Для нього справедлива формула:
ω = α × t
Це рівність справедливо лише тоді, коли α не є функцією часу, тобто α = const. Такий рух називається рівноприскореним.
Кут повороту для равноускоренного руху тіла з місця, тобто при відсутності початкової швидкості обертання, можна обчислити так:
θ = α × t2 / 2
Звідси отримуємо формулу кутового прискорення через центральний кут повороту:
α = (2 × θ) / t2
Зазначимо, якщо тіло спочатку оберталося без прискорення зі швидкістю ω0, а потім, почало рухатися прискорено, то для пройденого їм кутового відстані можна записати:
θ = ω0 × t + α × t2 / 2
Звідси нескладно отримати відповідний вираз для α.
Зв’язок між лінійним та кутовим прискоренням
Лінійне прискорення a показує приріст швидкості v за час t. Ця величина вимірюється в метрах за секунду квадратну, тобто:
a = dv / dt
Щоб знайти зв’язок між величинами a і α звернемося до наступної формулою, наведеною раніше:
L = θ × r
Візьмемо похідну від лівої та правої частини рівності за часом, отримаємо:
dL / dt = dθ / dt × r =>
v = ω × r
Візьмемо ще раз похідну за dt:
dv / dt = dω / dt × r =>
a = α × r
Ми отримали формулу зв’язку лінійного і кутового прискорення. Вираз показує, що при постійному прискоренні α, величина a буде лінійно зростати зі збільшенням радіуса обертання.
Рішення завдання
Відомо, що автомобіль рухається з лінійним прискоренням 2 м/с2. Необхідно визначити кутове прискорення його колеса, якщо діаметр колеса дорівнює 40 див.

Рішення цієї задачі можна виконати, провівши послідовні математичні викладки, і переходячи від лінійних характеристик до кутовим. Однак, вище було наведено рівність, що пов’язує величини a і α. Воно дозволяє записати формулу кутового прискорення колеса. Маємо:
a = α × r =>
α = 2 × a / d, де d = 2 × r.
Підставляємо дані з умови, записуємо відповідь: α = 10 рад/с2.