Будь-який контакт між двома тілами призводить до появи сили тертя. При цьому не важливо, в якому агрегатному стані речовини знаходяться тіла, вони рухаються відносно один одного або спочивають. У даній статті коротко розглянемо, які види тертя існують в природі і техніці.
Тертя спокою
Для багатьох може бути дивною думку, що тертя тіл існує навіть тоді, коли вони перебувають у стані спокою відносно один одного. Крім того, ця сила тертя є найбільшою за величиною силою серед інших видів. Проявляється вона тоді, коли ми намагаємося зрушити з місця якої-небудь предмет. Це може бути дерев’яний брусок, камінь і навіть колесо.
Причиною існування сили тертя спокою є наявність нерівностей на дотичних поверхнях, які механічно взаємодіють один з одним за принципом пік-западина.
Обчислюється сила тертя спокою за наступною формулою:
Ft1 = ut*N
Тут N – реакція опори, з якої на тіло впливає поверхню вздовж нормалі. Параметр ut є коефіцієнтом тертя. Він залежить від матеріалу дотичних поверхонь, якості обробки цих поверхонь, їх температури і від деяких інших факторів.
Записана формула свідчить, що від площі контакту сила тертя спокою не залежить. Вираз для Ft1 дозволяє розрахувати так звану максимальну силу. У ряді ж практичних випадків Ft1 не є максимальною. Вона завжди дорівнює за величиною зовнішньої сили, яка прагне вивести зі стану спокою тіло.
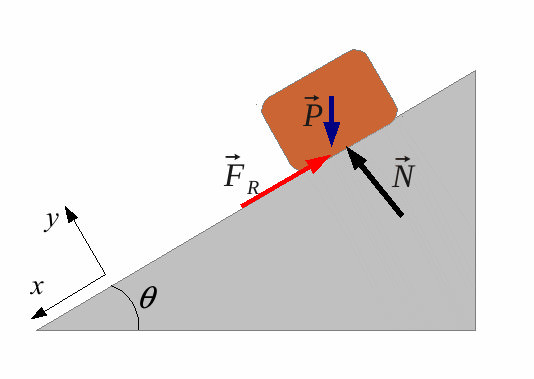
Тертя спокою відіграє важливу роль у житті. Завдяки цьому ми можемо рухатися по землі, відштовхуючись від неї підошвами ніг, не прослизаючи. Будь-які тіла, які знаходяться на похилих до горизонту площинах, не зісковзують з них завдяки силі Ft1.