Щоб читачеві було легше уявити собі, що таке гіперболоїд – тривимірний об’єкт, – спочатку треба розглянути однойменну криву гіперболу, помещающуюся у двовимірний простір.
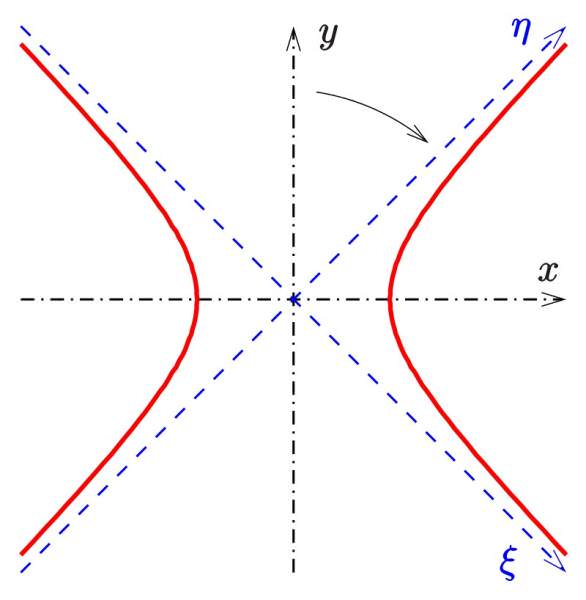
У гіперболи є дві осі: дійсна, на даному малюнку збігається з віссю абсцис, і уявна – з віссю ординат. Якщо подумки почати провертати рівняння гіперболи навколо її уявної осі, то поверхню, завіяна” кривий, складе з себе однополостной гіперболоїд.
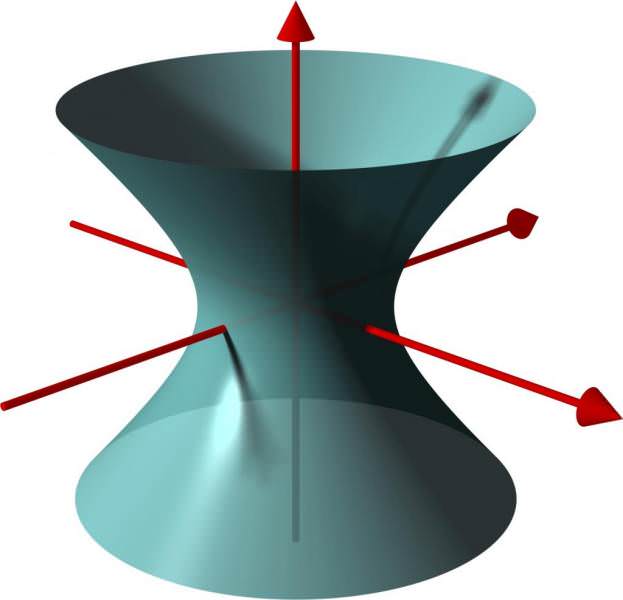
Якщо ж почати обертати таким чином гіперболу навколо її дійсної осі, то кожна з двох “половинок” кривий складе свою окрему поверхню, і разом це буде називатися двуполостным гиперболоидом.
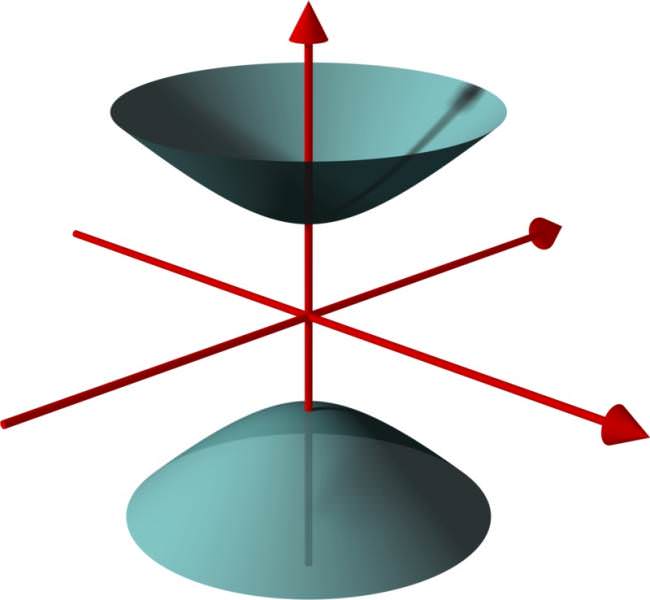
Отримані з допомогою обертання відповідної плоскої кривої, вони називаються відповідно гиперболоидами обертання. У них у всіх напрямках, перпендикулярних осі обертання, зберігаються параметри, що належать обертається кривої. В загальному випадку це не так.
Рівняння гіперболоїда
У загальному випадку поверхня може бути задано такими рівняннями в декартових координатах(x,y,z):

У разі гіперболоїда обертання його симетрія відносно осі, навколо якої оберталися, виражається в рівності коефіцієнтів a=b.
Характеристики гіперболоїда
У нього є фокус. Ми знаємо, що фокуси є у кривих на площині – у випадку з гіперболою, наприклад, модуль різниці відстаней від довільної точки, на гіперболи до фокуса і другого постійний за визначенням, власне, точок фокуса.
При переході в тривимірний простір визначення практично не змінюється: фокуси – це знову дві точки, і різниця відстаней від них до довільної точки, яка належить поверхні гіперболоїда, постійна. Як видно, із змін з’явилася тільки третя координата у всіх можливих точок, тому що тепер вони задаються в просторі. Взагалі кажучи, визначення фокусу еквівалентно виявлення типу кривої або поверхні: говорячи про те, як розташовані точки поверхні відносно фокусів, ми фактично відповідаємо на питання, що таке гіперболоїд і як він виглядає.
Варто згадати, що у гіперболи є асимптоти – прямі, до яких її гілки прагнуть на нескінченності. Якщо при побудові гіперболоїда обертання подумки обертати асимптоти разом з гіперболою, то крім гіперболоїда вийде ще й конус, званий асимптотичних. Асимптотичний конус є як у однополостных, так і у двуполостных гіперболоїдів.
Ще одна важлива характеристика, наявна лише у однополостного гіперболоїда, – прямолінійні твірні. Як видно з назви, це лінії, і вони повністю лежать на заданій поверхні. Через кожну точку однополостного гіперболоїда проходять дві прямолінійні твірні. Вони належать відповідно двом родинам прямих, які описуються наступними системами рівнянь:
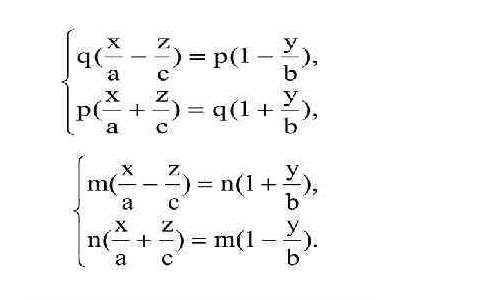
Таким чином, однополостный гіперболоїд цілком можна скласти з нескінченного числа прямих ліній двох родин, причому кожна лінія одного з них буде перетинатися з усіма лініями іншого. Поверхні, які відповідають таким властивостям, називаються лінійчатими; їх можна побудувати за допомогою обертання одній прямій. Визначення через взаємне розташування прямих (прямолінійних твірних) в просторі, також може служити однозначним позначенням того, що таке гіперболоїд.
Цікаві властивості гіперболоїда
Криві другого порядку і відповідні їм поверхні обертання кожна мають цікаві оптичні властивості, пов’язані з фокусами. У випадку з гиперболоидом це формулюється наступним чином: якщо з одного фокуса випустити промінь, відбившись від найближчої “стінки”, він прийме такий напрямок, як ніби йшов з другого фокуса.
Гіперболоїди в житті
Швидше за все, більшість читачів починали своє знайомство з аналітичної геометрії і поверхнями другого порядку з фантастичного роману Олексія Толстого “Гіперболоїд інженера Гаріна”. Однак письменник то сам добре не знав, що таке гіперболоїд, то пожертвував точністю в догоду художності: описуване винахід по фізичним характеристикам скоріше є параболоидом, який збирає всі промені в одному фокусі (в той час як оптичні властивості гіперболоїда пов’язані з розсіюванням променів).

В архітектурі дуже популярні так звані гиперболоидные конструкції: це споруди, за формою є однополостным гиперболоидом або гіперболічним параболоидом. Справа в тому, що тільки в цих поверхонь обертання другого порядку є прямолінійні твірні: таким чином, вигнуту конструкцію можна спорудити лише з прямих балок. Переваги таких конструкцій – у здатності витримувати великі навантаження, наприклад, від вітру: форму гіперболоїда використовують при будівництві високих споруд, наприклад, телевеж.