При вивченні поведінки газів у фізиці багато уваги приділяється изопроцессам, тобто таким переходів між станами системи, під час яких зберігається один термодинамічний параметр. Тим не менш, існує газовий перехід між станами, який не є изопроцессом, але який відіграє важливу роль в природі і техніці. Мова йде про адіабатичному процесі. У цій статті розглянемо його докладніше, акцентуючи увагу на тому, що таке показник адіабати газу.
Адіабатичний процес
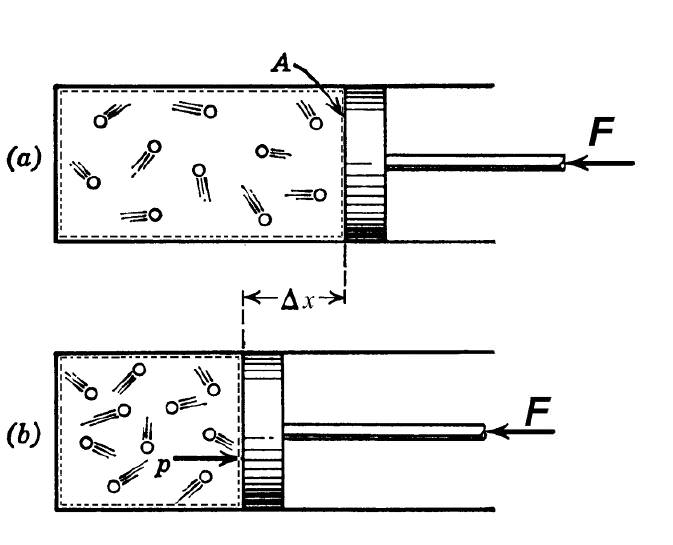
Згідно термодинамічному визначенням, під адіабатичним процесом розуміють такий перехід між початковим і кінцевим станами системи, в результаті якого не існує обміну теплом між зовнішнім середовищем і вивчається системою. Такий процес можливий при наявності двох наступних умов:
- теплопровідність між зовнішнім середовищем та системою з тієї чи іншої причини є низькою;
- швидкість процесу велика, тому обмін теплом не встигає відбуватися.
В техніці адиабатный перехід використовують як для розігрівання газу при його різкому стисненні, так і для його охолодження під час швидкого розширення. У природі розглянутий термодинамічний перехід проявляє себе, коли повітряна маса піднімається або опускається по схилу пагорба. Такі підйоми і спуски призводять до зміни точки роси в повітрі і до виникнення опадів.