Коли в школах вивчають стереометрії, то велика увага в навчальному процесі звертають на вивчення формул та методів розрахунку обсягу фігур у просторі. В даній статті розглянемо що таке призма, і наведемо формули для обчислення об’єму прямої призми.
Призма в стереометрії
Перш ніж розглядати формули визначення об’єму прямої призми, розберемо докладніше про який клас геометричних об’єктів піде мова. Призма – яскравий представник скоєних многогранників, в яких число сторін, вершин і ребер пов’язано рівнянням Ейлера.
У стереометрії дають таке просте визначення призмі: це такий багатогранник, в якому дві утворюють його межі є абсолютно однакові і знаходяться в паралельних площинах, а інші грані являють собою або паралелограми, або прямокутники (приватний випадок паралелограма).
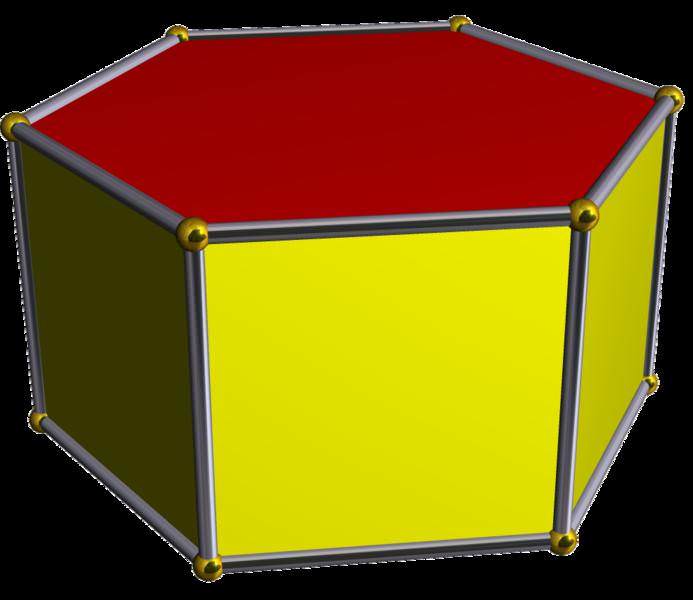
На малюнку показана шестикутна призма, в якій всі названі вище елементи виділені. Так, у неї 12 вершин, 18 ребер і 8 сторін або граней. Жовті боку в сукупності утворюють бічну поверхню, а червона грань – це основа фігури.
Геометрично будь-яка призма може бути отримана за допомогою такої нескладної методики. Необхідно взяти довільний багатокутник. Єдина умова полягає в тому, що багатокутник повинен бути плоским. Потім, з допомогою певного відрізка, який площини многокутника не належить, перенести всі його вершини нову паралельну площину. В результаті ми отримаємо каркас призми.
Види фігури і пряма призма
У стереометрії виділяють декілька типів класифікацій призм. Фігури цього класу розрізняють за кількістю сторін на підставі, по ввігнутості або випуклості підстави, за типом всіх граней бічній поверхні і по правильній формі підстави. Тут ми не ставимо завдання розглянути всі варіанти класифікації, а зосередимо свою увагу лише на прямих і похилих призмах.
Пряма або прямокутна призма – це такий многогранник, у якого всі бокові сторони, є прямокутниками або квадратами. Інше рівноправне з попереднім визначення призми свідчить: якщо всі бічні ребра перпендикулярні підстав, то має місце прямокутна фігура. Обома визначеннями можна користуватися при вирішенні практичних завдань, оскільки вони є достатніми і необхідними.
Якщо у прямій призмі підстави являють собою рівнокутні і рівносторонні багатокутники, то про таку фігуру кажуть, що вона правильна. З даних визначень зрозуміло, що будь-яка правильна призма буде прямокутної, але не всяка пряма фігура є правильною.
Формула об’єму прямої призми
У розглянутому вигляді призми довжина будь-якого бічного ребра дорівнює висоті h фігури. В той же час як для прямокутної, так і для похилої призми обсяг визначають за такою формулою:
V = So × h.
Де символом So позначена площа однієї підстави. Якщо буквою b позначити довжину бічного ребра, тоді це вираз для прямої фігури можна переписати у вигляді:
V = So × b.
Як випливає з цих рівностей, все питання визначення величини V полягає в обчисленні площі So. Природно, що не існує якоїсь певної формули для її визначення, оскільки на підставі може перебувати багатокутник абсолютно довільного типу. Тим не менш, для деяких фігур конкретні формули можна записати.
Наприклад, якщо пряма призма є правильною, тоді для So справедлива формула:
So = n / 4 × ctg(pi / n) × a2.
Де n a – число сторін і довжина однієї сторони, відповідно.
Інший приклад, коли можна привести конкретну формулу, це трикутне основу. Якщо відомі довжина сторони a і висота трикутника, опущена на неї, ha, тоді площа So розраховується так:
So = 1 / 2 × a × ha.
Звернемо увагу, що при використанні формули для V фігури, слід в неї підставляти площа одного, а не двох підстав.
Приклад розв’язання задачі
Необхідно визначити об’єм прямої призми, основою якої є прямокутний трикутник. Гіпотенуза трикутника дорівнює 12 см, а один з його катетів становить 4 см. Висота об’ємної фігури дорівнює 10 див.
З курсу планіметрії кожен школяр знає, що половина твору катетів дають площа відповідного трикутника. Користуючись теоремою Піфагора, отримуємо другий катет:
a2 = √(c2 – a12) = √(122 – 42) = 11,31 див.
Тоді площа So трикутника складе:
So = 4 × 11,31 / 2 = 22,62 см2.
Застосовуючи формулу для об’єму, отримуємо:
V = 22,62 × 10 = 226,2 см3.
Таким чином, об’єм прямої призми дорівнює 226,2 см3.












