Всі фігури, які обмежені гранями, що перебувають у різних площинах в просторі, володіють певним обсягом. Обчисленням цієї величини займається спеціальний геометричний розділ – стереометрія. У цій статті наведемо формулу обсягу шестикутної призми.
Що таке призма?
Очевидно, що перш ніж знаходити об’єм геометричної фігури, слід познайомитися з нею і зрозуміти, якими властивостями вона володіє. В даному випадку мова йде про призмі. У стереометрії для цієї фігури наводиться наступне визначення: призмою називається будь-просторовий геометричний об’єкт, який обмежений двома n-косинцями, що знаходяться в паралельних площинах, і n параллелограммами. Тут n – будь-яке натуральне число починаючи з трьох.
Побудувати фігуру нескладно. Для цього слід взяти довільний багатокутник і за допомогою однакових паралельних один одному відрізків перенести його в іншу площину. Отримана фігура буде призмою. Відзначимо, що вона, на відміну від конуса, циліндра і сфери, не є фігурою обертання, тобто її не можна отримати з допомогою обертання навколо осі будь-якої плоскої фігури.

Вище на малюнку наведено для прикладу паралелепіпед, який є чотирикутної призмою.
Шестикутна Призма і її види
Далі в статті наведемо формулу обсягу шестикутної призми. Що являє собою ця фігура? Будь-яка призма, що має в основі шестикутник, називається шестикутної.
Вона утворена двома шестикутниками в підставах і шістьма параллелограммами, сукупність яких становить бічну площа фігури. Ця призма має 12 вершин, 8 граней або сторін і 18 ребер, 2/3 з яких належать підстав.
Наведеним описом елементів відповідають кілька видів шестикутної призми. По-перше, ця фігура може бути опуклою або увігнутою, що залежить від шестикутника на підставах, по-друге, призма може бути похилій і прямий. Різниця між ними полягає в тому, що в прямій фігурі будь-бічна сторона буде перпендикулярна підстав, а в похилій фігурі бокові сторони перетинають підстави під деякими кутами, які відмінні від 90o. Обидві призми показано на рисунку.
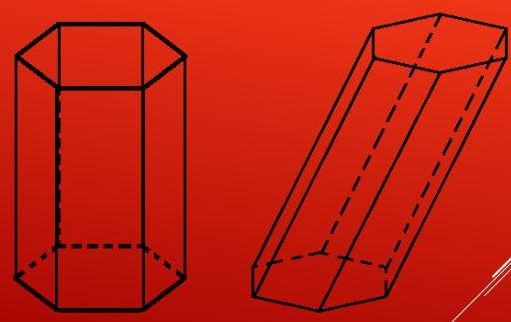
Зауважимо, що умова перпендикулярності бічних сторін і підстав призводить до того, що паралелограми прямої призми стають прямими.
Нарешті, по-третє, шестикутна призма буває правильною і неправильною. Останній буде будь-яка фігура, яка не є прямою і не має правильним шестикутним підставою. Далі основну увагу будемо приділяти саме правильної призми.
Правильний шестикутник
Для визначення об’ємів геометричних фігур багатьох класів необхідно знати значення площі їх основи. Цей факт справедливий для пірамід, циліндрів, конусів. Призми теж не є винятком.
Щоб знайти площу основи шестикутної призми, слід розрахувати площа шестикутника. Найпростіше зробити це для правильної фігури. Для наочності покажемо, що таке правильний шестикутник.
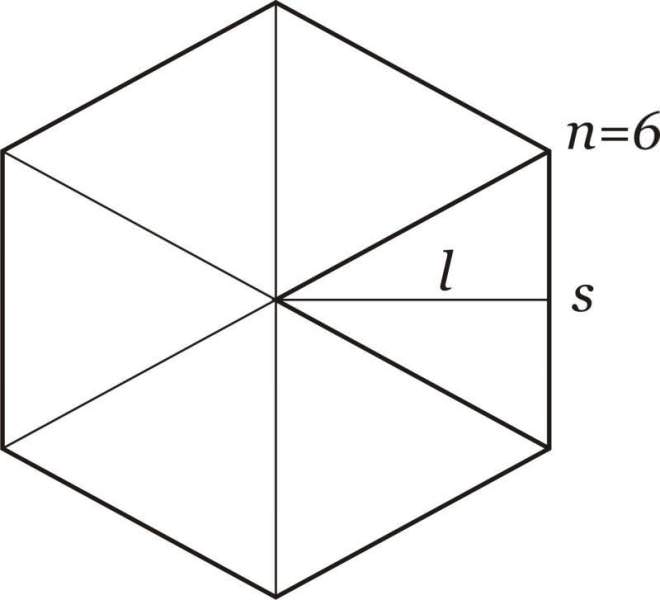
Видно, що представляє він багатокутник, утворений шістьма однаковими сторонами, які перетинаються під кутами 120 o. Також видно, що в шестикутник можна вписати окружність деякого радіуса, а також можна описати його колом.
Обчислення площі основи призми правильної шестикутної зводиться до визначення площі наведеної вище фігури. Якщо шестикутник розбити на рівносторонні трикутники так, як показано на малюнку, то його площа дорівнює помноженої на 6 площі одного трикутника. Позначимо довжину сторони шестикутника буквою a, тоді для площі S шестикутника отримуємо:
S = 6*1/2*a*√3/2*a = 3*√3/2*a2.
Для будь-якого іншого шестикутника, який не є правильним, ця формула буде несправедливою.
Формула обсягу шестикутної призми
Обчислити обсяг будь призми нескладно, для цього слід знати всього два її параметри: висоту h і підстави площа S. Розрахунок обсягу V здійснюється по наступній формулі:
V = h*S.
Відзначимо важливу річ: записане вираз справедливий для будь-яких видів призм, включаючи увігнуті і похилі. Тим не менше для довільної призми, незважаючи на простоту формули, застосовувати її буває складно. Складність пов’язана з визначенням обох параметрів у виразі.
У зв’язку з вищесказаним, розглянемо конкретну правильну призму з правильним шестикутним підставою. Якщо її висота дорівнює h, а довжина сторони дорівнює a, тоді формула обсягу шестикутної призми правильної прийме вигляд:
V = 3*√3/2*h*a2.
При записі цього виразу була підставлена формулу для S, наведена в попередньому пункті.
Далі вирішимо два завдання, в яких покажемо, як знайти об’єм шестикутної призми для конкретних випадків.
Завдання з відомою діагоналлю
Нижче на малюнку показана правильна призма. Відомо, що сторона її підстави дорівнює 9 див. Чому дорівнює об’єм шестикутної призми, якщо діагональ AB має довжину 21 див.
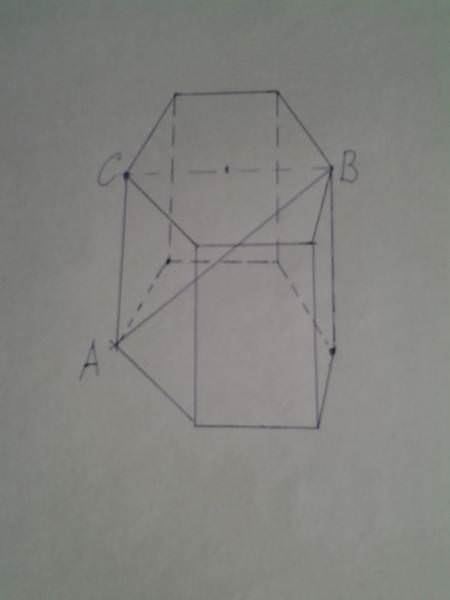
Не складно здогадатися, глянувши на малюнок, що трикутник ABC є прямокутним, причому сторона AB – це гіпотенуза. Катет AC є висотою h фігури. Щоб обчислити об’єм призми, нам необхідно знайти довжину цього катета. Зауважимо, що другий катет CB має у два рази більшу довжину, ніж сторона підстави, тобто 18 див. Застосовуємо теорему Піфагора і отримуємо:
h = AC = √(AB2-CB2) = √(212-182) ≈ 10,82 див.
Значення висоти ми округлили до сотих часток сантиметра.
Оскільки нам відома висота h і сторона підстави a, то можна застосувати формулу для V. Отримуємо:
V = 3*√3/2*h*a2 = 3*√3/2*10,82*92 = 2277 см3.
Таким чином, розглянута призма має обсяг майже 2,3 літра.
Завдання з вписаним в призму циліндром
Відомо, що циліндр з радіусом 12 см вписаний в правильну шестикутну призму. Об’єм циліндра дорівнює 1360 см3. Чому дорівнює об’єм призми?

Як було показано, визначити об’єм призми можна, якщо знати її висоту і сторону основи. Почнемо з визначення сторони. Оскільки радіус r кола, вписаного в шестикутник, відомий, значить, довжину сторони a можна розрахувати так:
a = 2*r/√3.
Зрозуміти, звідки взялася ця формула, можна, якщо врахувати, що радіус r є заввишки одного з шести рівносторонніх трикутників шестикутника.
Тепер обчислимо висоту h призми. Згідно з умовою задачі, вона повинна збігатися з висотою циліндра. Об’єм циліндра розраховується за тією ж формулою, що і для призми. Маємо:
Vc = So*h = pi*r2*h =>
h = Vc/(pi*r2).
Підставляємо вирази для a і h у формулу для V призми, отримуємо:
V = 3*√3/2*h*a2 = 3*√3/2*Vc/(pi*r2)*(2*r/√3)**2 = 2*√3*Vc/pi.
Ми прийшли до цікавого результату: виявляється, обсяг шестикутної призми не залежить від радіуса вписаного циліндра, а однозначно визначається його об’ємом. Підставивши значення Vc, отримуємо об’єм призми, рівний приблизно 1500 см3.