При вивченні стереометрії в старших класах шкіл розглядають властивості фігур у просторі. Одним з основних властивостей є обсяг, проте іноді виникають геометричні проблеми, які вимагають обчислення площ поверхонь фігур. У цій статті розглянемо конкретне питання: за якою формулою площа бічної поверхні трикутної призми можна знайти?
Трикутна призма
Для початку розберемося, яка фігура буде розглянута в статті. Призма – це такий геометричний об’єкт, який складається з двох однакових паралельних багатокутних граней і декількох довільних паралелограмів, які зазначені межі з’єднують між собою. Побудувати призму нескладно. Для цього достатньо взяти n-кутник плоский і паралельно самому собі перенести його в іншу площину. У процесі переносу боку n-кутника опишуть всі паралелограми фігури, сукупність яких утворює бічну поверхню призми. Самі ж n-кутники називаються її підставами.
Тут ми не будемо розглядати всі можливі види призм, а зосередимо свою увагу на трикутної фігури. Нескладно здогадатися, що під нею розуміють таку призму, n-вугільні заснування якої є трикутниками. Причому трикутники можуть бути самої різної форми, включаючи рівнобедрені і рівносторонні.
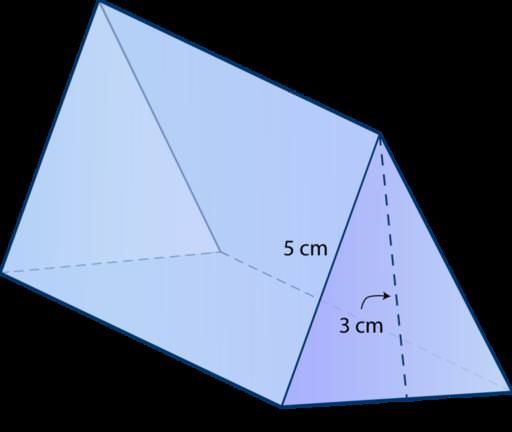
Таким чином, трикутна призма утворена п’ятьма гранями (2 трикутника і 3 паралелограма). Фігура має 6 рівноправних вершин і 9 ребер двох видів: ребра підстави і ребра бічній поверхні. Вище показано приклад такої призми.
Види трикутних призм
Розглянута фігура є найпростішою серед призм, оскільки трикутник – це підстава з найменшою можливою кількістю сторін. Будь-яка трикутна призма є опуклою. У загальному випадку можна виділити три види цієї геометричної фігури:
- похила;
- пряма;
- правильна.
Щоб розуміти різницю між зазначеними видами, слід звернути увагу на тип підстави і бічних сторін. Так, якщо бічні сторони є параллелограммами загальної форми або ромбами, то призма однозначно буде похилою. Якщо ж всі бічні грані утворені прямими або квадратами, то перед нами пряма призма. Остання може бути правильною, якщо всі три прямокутники є однаковими. Інший критерій правильності прямий фігури полягає в тому, що у неї правильним є підстава, тобто воно утворене трикутник з рівними сторонами.
Далі розглянемо формули площі бічної поверхні правильної трикутної призми, прямий, похилій і відсіченої.
Похила призма
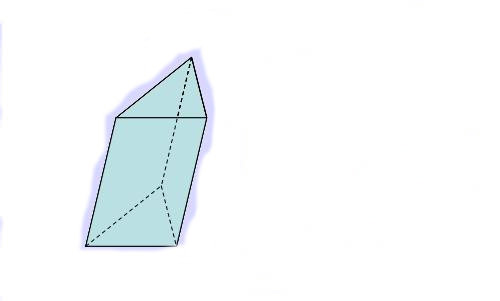
Мова йде про трикутної фігури довільного виду. Обчислити площу бічної поверхні для неї найважче, оскільки висота h фігури (дистанція між підставами) не збігається з довжиною бічного ребра b.
Якщо виникає задача визначення площі поверхні (бічний) такої призми, то поступають таким чином: спочатку роблять уявний зріз фігури, який повинен бути перпендикулярний всім бічних ребер і граней. Потім розраховують периметр цього зрізу. В даному випадку мова йде про периметр трикутника. Припустимо, що він дорівнює Psr. Площа бічної поверхні визначається шляхом множення величини Psr на сторону b, тобто має місце наступна формула:
Sb = Psr × b
Пряма призма
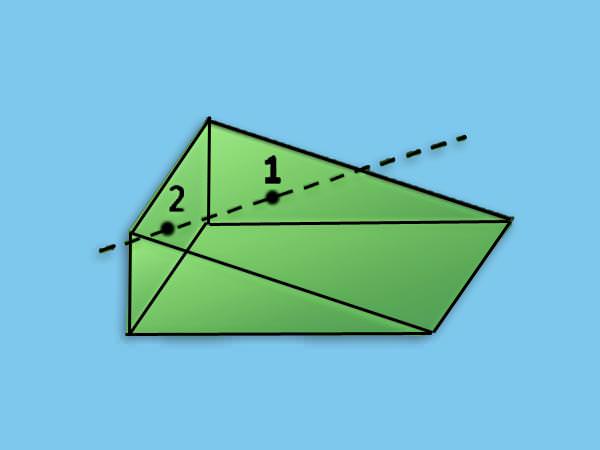
Як вище було сказано, бічна поверхня цієї призми утворена трьома прямокутниками. Дві сторони цих прямокутників є однаковими, вони дорівнюють довжині бічного ребра b, який також є висотою h фігури. Що стосується останніх двох сторін, то вони можуть відрізнятися. Ці сторони є сторонами підстав. Позначимо їх символом ai, де i = 1, 2, 3. Тоді формула площі поверхні бічної прямої трикутної призми запишеться так:
Sb = b × ∑i=13ai
Багато могли помітити, що цей вираз не відрізняється від аналогічного для похилої призми, адже сума трьох сторін ai є периметром підстави. Це пов’язано з тим, що для прямої фігури підстава є перпендикулярним бічним граням зрізом.
Правильна фігура
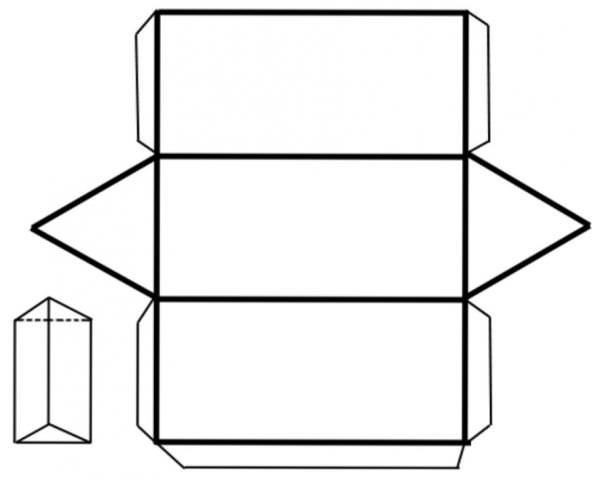
Формула площі поверхні бічної трикутної призми правильною є найпростішою порівняно з виразами вище. У правильної фігури всі бічні грані є не просто прямокутниками (квадратами в деяких випадках), але ще вони рівні між собою. Ці геометричні факти дозволяють записати формулу площі поверхні бічної призми правильної трикутної в такому вигляді:
Sb = 3 × a × b
Тут a – сторона підстави (трикутника). Цифра 3 з’являється тому, що бічна поверхня представлена трьома рівними гранями. Нагадаємо, що в даному виразі сторона b може бути замінена висотою h.
Очевидно, якщо бокові сторони представляють собою квадрати, то формула для Sb запишеться так:
Sb = 3 × a2
Відсічена фігура
Така призма утворюється, якщо з допомогою площині відсікти її частина. Якщо січна площина паралельна підстав, то формула площі бічної поверхні трикутної призми відсіченої прийме один із записаних в попередніх пунктах вигляд. Дійсно, при паралельному перерізі ми отримаємо аналогічну за формою вихідної призмі фігуру.
Якщо ж січна площина не паралельна підстав, тоді для визначення площі відсіченої призми необхідно буде проводити спеціальний геометричний аналіз, оскільки її бічна поверхня буде представлена неправильними чотирикутниками.