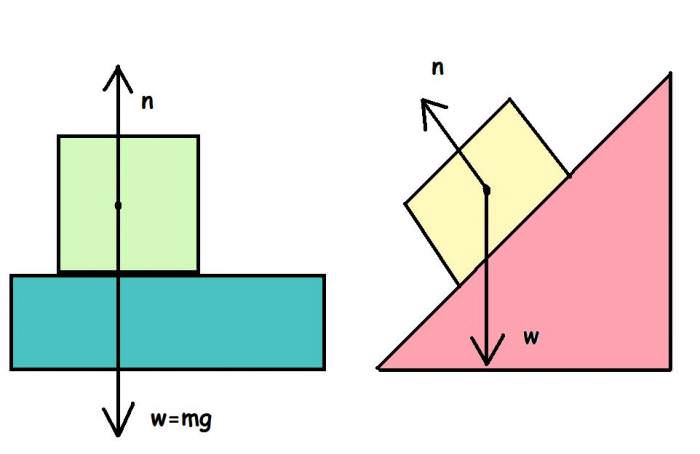
У загальному курсі фізики вивчають два найбільш простих типу переміщення об’єктів у просторі – це поступальний рух і обертання. Якщо динаміка поступального руху заснована на використанні таких величин, як сили і маси, то для кількісного опису обертання тіл використовують поняття моментів. У цій статті розглянемо, за якою формулою момент сили обчислюють, і для рішення яких завдань користуються цією величиною.
Момент сили
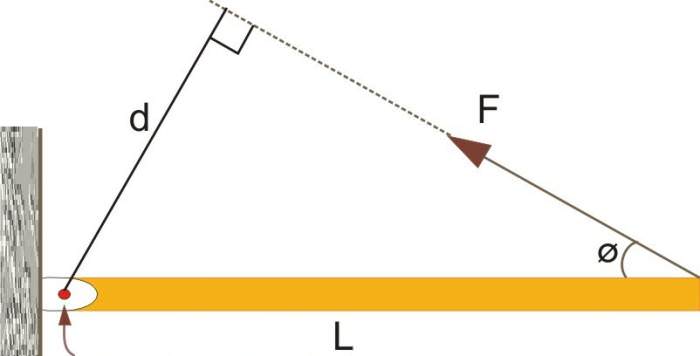
Уявимо собі просту систему, яка складається з матеріальної точки, що обертається навколо осі на відстані r від неї. Якщо до цієї точки докласти дотичну силу F, яка буде перпендикулярна осі обертання, то вона призведе до появи кутового прискорення точки. Здатність сили призводити до обертальному руху систему називається крутним моментом або моментом сили. Обчислюють за наступною формулою:
M = [r*F]
У квадратних дужках варто векторний добуток радіус-вектора на силу. Радіус-вектор r є спрямованим відрізком від осі обертання до точки додатка вектора F. Враховуючи властивість векторного добутку, для значення модуля моменту формула у фізиці запишеться в такому вигляді:
M = r*F*sin(φ) = F*d, де d = r*sin(φ).
Тут кут між векторами r і F позначений грецькою буквою φ. Величина d називається плечем сили. Чим воно більше, тим більший крутний момент може створити сила. Наприклад, якщо відкривати двері, натискаючи на неї поблизу петель, то плече d буде маленьким, тому необхідно докласти велику силу, щоб повернути двері на петлях.
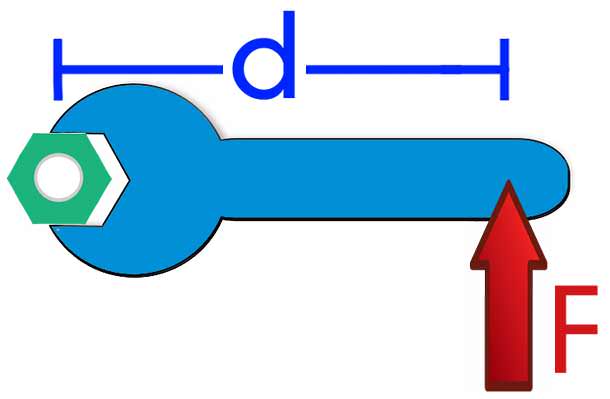
Як видно з формули моменту, величина M – це вектор. Спрямований він перпендикулярно до площини, в якій лежать вектори r і F. Напрямок M легко визначити з використанням правила правої руки. Щоб ним скористатися, необхідно чотири пальці правої руки спрямувати вздовж вектора r за напрямом дії сили F. Тоді відігнутий великий палець покаже напрям моменту сили.
Момент сили в статиці

Розглянута величина є дуже важливою при обчисленні умов рівноваги системи тіл, що мають вісь обертання. Таких умов в статиці всього два:
- рівність нулю всіх зовнішніх сил, які впливають на систему той чи інший вплив;
- рівність нулю моментів сил, пов’язаних із зовнішніми силами.
Обидва умови рівноваги математично можна записати так:
∑i(Fi) = 0;
∑i(Mi) = 0.
Як видно, обчислювати необхідно саме векторну суму величин. Що стосується моменту сили, то прийнято вважати його позитивний напрямок, якщо сила робить поворот проти ходу стрілки годинника. В іншому випадку перед формулою визначення моменту слід використовувати знак мінус.
Зазначимо, якщо в системі вісь обертання розташована на деякій опорі, то відповідна сила реакції моменту не створює, оскільки її плече дорівнює нулю.
Момент сили в динаміці
Динаміка руху обертання навколо осі має так само, як і динаміка поступального переміщення, основне рівняння, на основі якого вирішуються багато практичні завдання. Воно називається рівнянням моментів. Відповідна Формула записується у вигляді:
M = I*α.
По суті, цей вираз є другим законом Ньютона, якщо момент сили замінити на силу, момент інерції I – на масу, а кутове прискорення α – на аналогічну лінійну характеристику. Щоб краще розуміти це рівняння, зазначимо, що момент інерції виконує ту ж саму роль, що звичайна маса при поступальному русі. Момент інерції залежить від розподілу маси в системі відносно осі обертання. Чим більше відстань тіла до осі, тим більше величина I.
Кутове прискорення α обчислюється в радіанах в секунду в квадраті. Воно характеризує швидкість зміни обертання.
Якщо момент сили дорівнює нулю, тоді система не отримує ніякого прискорення, що свідчить про збереження моменту імпульсу.
Робота моменту сили

Оскільки вивчається величина вимірюється в ньютонах на метр (Н*м), то багато хто може подумати, що її можна замінити джоулем (Дж). Однак цього не роблять тому, що вимірюється в джоулях деяка енергетична величина, момент сили – це силова характеристика.
Так само як сила, момент M теж може здійснювати роботу. Обчислюється вона за такою формулою:
A = M*θ.
Де грецькою буквою θ позначений кут повороту в радіанах, на який повернулася система в результаті дії моменту M. Зауважимо, що в результаті множення моменту сили на кут θ, одиниці вимірювання зберігаються, проте, вже використовують саме одиниці роботи, тобто, Джоулі.