Кожен школяр знайомий з рівномірним рухом, що для його опису передбачає знання лише значення швидкості тіла. Проте в природі найчастіше поширене нерівномірний, прискорений рух. Розглянемо у статті, що таке прискорення, чому воно виникає при переміщенні тіл, і наведемо формули прискорення.
Історичне вивчення питання руху
Ні для кого не секрет, що навколишній нас світ перебуває в стані постійного руху і обертання. Незважаючи на це, наукове вивчення процесу переміщення тіл у просторі почалося відносно недавно. Так, філософи античної Греції вважали, що рух – це неприродний стан об’єктів (Зенон, Архімед, Арістотель).
З початком епохи Відродження, в результаті накопичення експериментальних даних, люди стали змінювати свій погляд на питання руху. Одним з перших вчених у світі, який довів, що рівномірний прямолінійний переміщення є природним станом оточуючих тіл, був Галілей. Згодом Ісаак Ньютон розширив його подання, створивши потужну і повну теорію опису руху і його причин – класичну механіку.
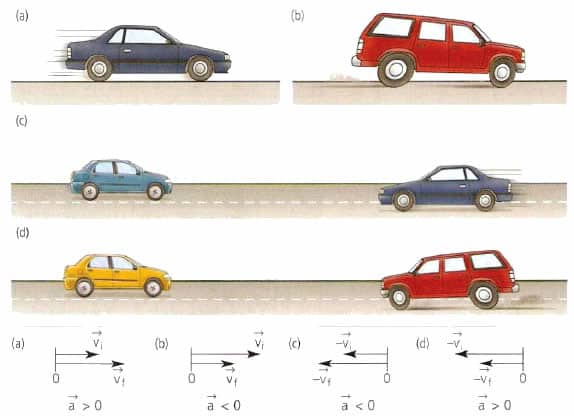
Другий закон Ньютона і прискорення
З першого року вивчення фізики в школах починають розглядати закони Ньютона.Вони містять відповідь на питання, чому з’являється прискорення тел. у Запишемо 2-й ньютонівський закон у звичній формі:
F = m*a.
Звідки формула прискорення тіла запишеться у вигляді:
a = F/m.
Цей вираз означає, що причиною виникнення прискорення тіл є зовнішня сила абсолютно будь-якої природи, яка впливає на тіла. Чим більше сила, тим більше значення буде мати прискорення. З іншого боку, чим більше маса тіла, тим менше прискорення зможе повідомити йому певна сила.
Записана формула прискорення тіла містить ще один важливий висновок: вектор a спрямований у ту ж сторону, що і вектор F, при цьому довжини цих векторів відрізняються на коефіцієнт пропорційності, який представляє собою масу m.
Кінематика руху з постійним прискоренням
Вище була записана формула прискорення руху, однак, не було дано визначення цієї величини. Під прискоренням у фізиці вважають швидкість, з якою в ході переміщення тіла змінюється його швидкість. Математично це можна записати так:
a = dv/dt.
Прискорення являє собою похідну від швидкості за часом. Ця формула є справедливою для абсолютно будь-якого виду руху, включаючи нерівномірне і криволінійне переміщення, наприклад, обертання по колу.
Якщо тіло рухається з постійним прискоренням, а його початкова швидкість дорівнює нулю, тоді справедливі наступні формули:
v = a*t;
S = a*t2/2.
Обидва вирази є основними формулами кінематики равноускоренного руху, тобто такого переміщення тіла, при якому його прискорення є постійною величиною.
Крім прискореного руху, часто доводиться вирішувати завдання на равнозамедленное рух, яке виникає при гальмуванні тел. У цьому випадку справедливі такі формули:
v = v0 – a*t;
S = v0*t – a*t2/2.
Тут v0 – швидкість тіла до моменту, коли почалося гальмування.
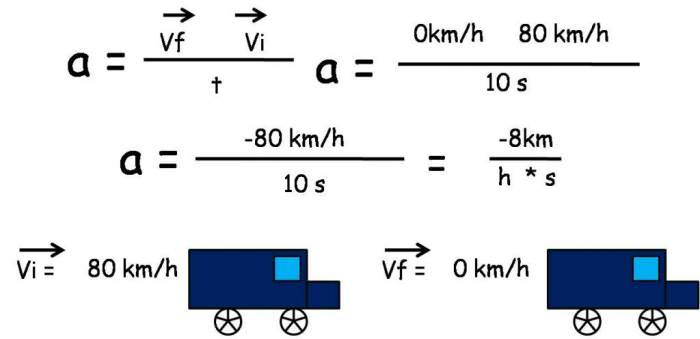
Неважко з представлених формул отримати відповідний вираз для прискорення. Так, у разі равнозамедленного переміщення отримуємо:
a = (v0 – v)/t;
a = 2*(v0*t – S)/t2.
Обертання по колу і прискорення
На відміну від прямолінійного переміщення, під час обертання змінюється не тільки модуль, але і напрямок швидкості. Взявши похідну від неї по часу, можна отримати дві різні складові повного прискорення, вони називаються тангенціальним і нормальним прискореннями (at і an).
Формула тангенціального прискорення не відрізняється від наведеної вище, тобто:
at = dv/dt.
Величина at описує зміну абсолютного значення швидкості і спрямована по дотичній до траєкторії (окружності).
Нормальне прискорення an описує зміну вектора швидкості, а не її абсолютної величини. Воно спрямоване до центра кривизни траєкторії (до центру кола), тому називається також доцентровим. Формула для його розрахунку має вигляд:
an = v2/r.
Де r – радіус кривизни траєкторії. Як показує це рівність, для появи an достатньо, щоб вектор швидкості змінював свій напрям, сама швидкість при цьому може залишатися постійною. Яскравим прикладом рівномірного руху по колу з певним доцентровим прискоренням є обертання Землі навколо осі або навколо Сонця.

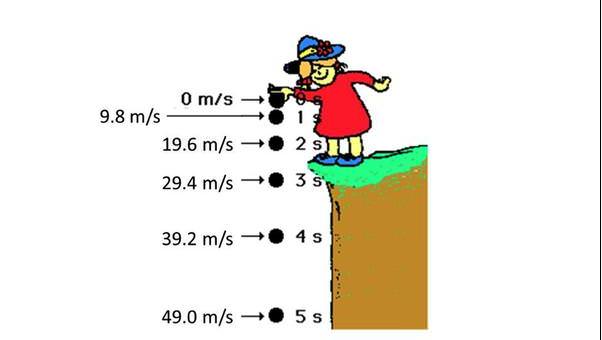
Прискорення вільного падіння
Це прискорення позначають літерою g у фізиці. Його поява пов’язана з дією сили тяжіння або гравітації масивних об’єктів (планет, зірок, галактик). Стосовно до нашої Землі можна сказати, що вона всім тілам в процесі їх падіння поблизу поверхні повідомляє прискорення 9,81 м/с2 (за кожну секунду швидкість збільшується на 9,81 м/с).
У реальності цей факт важко спостерігати на легких предметах, так як на них при падінні діє сила опору повітря.
Через вага тіла P, формула прискорення вільного падіння g прийме вигляд:
g = P/m.
Через рівняння кінематики равноускоренного руху, прискорення g можна розрахувати так:
h = g*t2/2 =>
g = 2*h/t2.
Де h – висота падіння тіла. Останню формулу Галілей використовував для експериментального визначення значення g.