Одним з многогранників, які вивчають у школах в курсі просторової геометрії, є піраміда. Ця фігура має ряд параметрів і характеристик, для обчислення яких використовують певні математичні формули. Прочитавши статтю, ви дізнаєтеся, як знаходити площу поверхні піраміди.
Що являє собою піраміда? Види фігури
Мова йде про фігуру в тривимірному просторі, яка являє собою многогранник, який складається з трикутників і багатокутника. Якщо взяти довільний багатокутник на площині і з’єднати всі його вершини прямими відрізками з якою-небудь точкою, яка не належить площині цього багатокутника, то ми отримаємо піраміду довільного типу.
Піраміда складається з граней, вершин і ребер. Межі являють собою площині, що обмежують обсяг фігури. Межі розділені один від одного ребрами. Якщо три грані перетинаються в одній точці, то остання є вершиною. Будь-яка така фігура має кілька вершин, наприклад, у трикутної фігури їх чотири, а в чотирикутної – п’ять. У кожної піраміди є тільки одна вершина, яка не належить основи. Вона називається головною чи основною.
Клас пірамід включає декілька типів фігур. Піраміда буде прямою, якщо її бічні трикутники є равнобедренными. Якщо ці трикутники ще й дорівнюють один одному, тоді фігура буде правильною. У будь прямий і правильної піраміди висота (відстань від головної вершини до підстави) перетинає основу в його геометричному центрі. Крім того, правильна фігура володіє рівностороннім (рівнокутним) підставою.
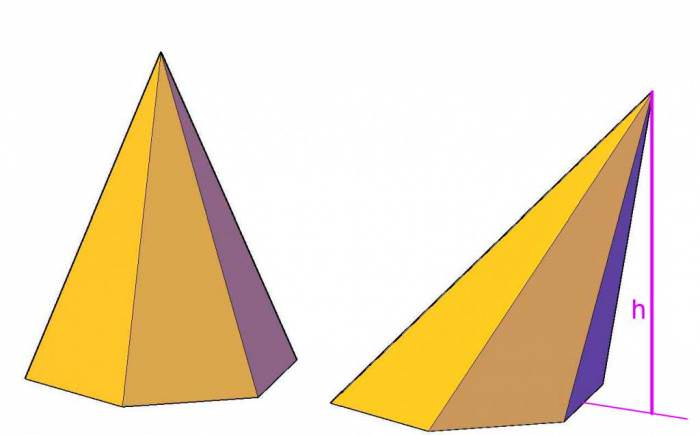
Площа поверхні піраміди
Під площею будь-подібної фігури розуміють суму площ всіх її сторін. Оскільки піраміди мають різний тип, то для розрахунку їх площ не існує універсальної формули. Однак існують вирази, які можуть бути використані в кожному конкретному випадку.
Якою б не була піраміда, вона завжди складається з n-вугільної межі і n трикутників. Площа трикутників обчислити нескладно, якщо відомі їх висоти та сторони основи. Що стосується n-кутника, то для визначення його площі слід провести аналіз, що це за n-кутник, чи є він правильним, які його кути відомі. Універсальним методом визначення його площі є розбиття на більш прості фігури, наприклад, трикутники або паралелограми.

Правильна фігура
Для правильної піраміди формула площі поверхні давно вже визначена. Перш ніж її записувати, зазначимо, що площа правильного підстави фігури може бути обчислена так:
Sn = n/4*a2*ctg(pi/n).
У формулою: a – сторона багатокутника, n – число сторін у ньому. Наприклад, для трикутника формула виглядає наступним чином:
S3 = √3/4*a2.
Для квадрата отримуємо типове рівність:
S4 = a2
Для правильної піраміди площа поверхні бічної Sb може бути визначена за такою формулою:
Sb = n/2*hb*a.
Де hb – апофема піраміди (висота бічного трикутника).
Складаючи вирази для Sn і Sb, отримуємо формулу площі повної поверхні піраміди:
S = Sn + Sb = n/4*a2*ctg(pi/n) + n/2*hb*a.
Зазначимо, що для однозначного визначення S будь піраміди правильної необхідно знати дві її лінійних параметра.
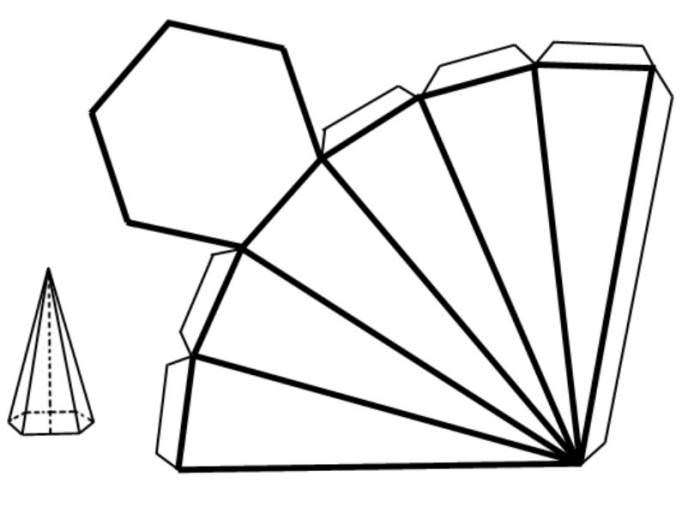
Похила фігура
Площа поверхні піраміди похилій розрахувати значно складніше, ніж правильною. Тим не менше, знаючи її розгортку, завжди можна вирішити поставлену задачу. Бічна поверхня похилій фігури розраховується так:
Sb = 1/2*∑i=1n(ai*hbi).
Тут ai – довжина i-ї сторони підстави, hbi – довжина i-ї апофемы. Апофемы для похилої піраміди загального типу розрізняються.
Площа підстави So обчислюється, виходячи з його типу, наприклад, якщо це паралелограм зі сторонами a1 і a2 і кутом між ними θ, тоді можна записати:
So = a1*a2*sin(θ).
Як для похилої, так і для прямої піраміди апофемы пов’язані з довжинами бічних ребер і ребер підстави. Цей зв’язок часто використовують при рішенні задач.