Тригонометрії – один з найважливіших розділів вивчення алгебри і геометрії, який необхідно зрозуміти і засвоїти навчаються. Свій початок дана наука бере аж у II-III тисячоліттях до нашої ери, коли вперше був здійснений спосіб вимірювання кута з використанням його градусної заходи. Швидше за все, ви вже знайомі з поняттями синуса кута, косинуса кута і знаєте їх табличні значення. Також, найімовірніше, ви вже зустрічалися з поняттям тангенса кута і його табличними значеннями відповідно.
Новий термін, з яким ми познайомимося в цій статті, – це котангенс.
Визначення
Алгебраїчне визначення:
котангенс кута – це відношення косинуса кута до синуса кута.
Геометричне визначення:
у прямокутному трикутнику для одного з його гострих кутів його котангенс – відношення прилеглого до нього катета до протилежного катету.
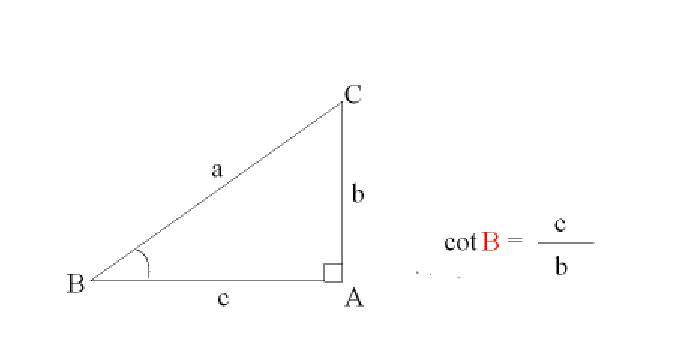
Згадаймо вже пройдені умовні позначення косинуса, синуса на листі, а також введемо нове письмове умовне позначення для котангенса:
- синус – sin;
- cos – cos;
- котангенс – ctg.
Нагадаємо читачеві, що котангенс – це тригонометрична функція.
Який зв’язок існує між тангенсом і котангенсом?
Котангенс – це зворотна функція від тангенса. Виходячи з цього, можна зазначити, що ставлення котангенса до тангенсу і навпаки завжди дорівнює одиниці: tg/ctg=1.
Який зв’язок існує між котангенсом і синусом?
Крім основної зв’язку між котангенсом і синусом через визначення (ctg = cos/sin) з допомогою тригонометричних перетворень можна вивести ще одну формулу без участі в ній косинуса: ctg2+1=1/sin2.
Виконаємо доказ наведеної вище формули:
- перетворимо ліву частину, використовуючи визначення котангенса: cos2/sin2+1;
- підведемо суму під одну дробову риску: (sin2+cos2)/sin2;
- застосувавши знання основного тригонометричного тотожності отримуємо: 1/sin2.
Отриманий вираз тотожно дорівнює правій частині формули, що і було потрібно довести.
Табличні значення котангенса
Як і інші тригонометричні функції, котангенс теж має свої табличні значення для кутів 0, 30, 45, 60, 90 градусів і похідних від них. Звичайно, всі ці значення можна обчислити через ставлення табличних значень косинуса і синуса, однак набагато зручніше запам’ятати значення даної функції, не вдаючись кожен раз при необхідності до обчислень.

Висновок
Сподіваємося, що дана стаття була вам корисною і допомогла зрозуміти, що це – котангенс. Якщо це так, то вам відкрита дорога для подальшого вивчення дивного світу тригонометрії. А нам, у свою чергу, залишається тільки побажати вам удачі в цьому нелегкому, але цікавому шляху!