Площина, поряд з точкою та прямою лінією, є базовим геометричним елементом. З його використанням будуються багато фігури в просторової геометрії. В даній статті розглянемо детальніше питання про те, як між двома площинами кут знайти.
Поняття
Перш ніж говорити про кут між двома площинами, слід добре розібратися, про якому елементі в геометрії піде мова. Розберемося з термінологією. Площина являє собою нескінченну сукупність точок у просторі, поєднуючи між собою які, ми отримаємо вектора. Останні будуть по відношенню до деякого одного вектора перпендикулярні. Його прийнято називати нормаллю до площини.
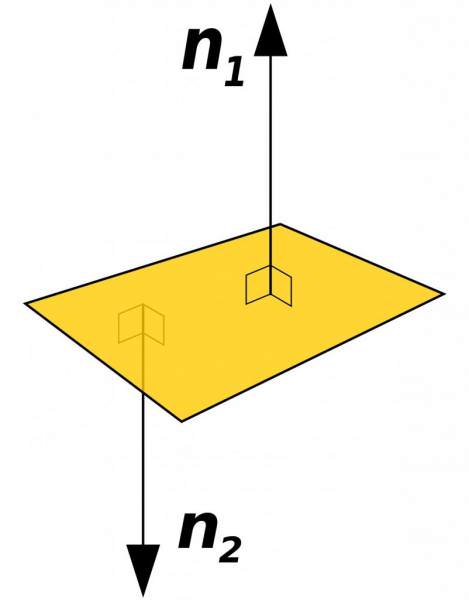
На малюнку вище показано площину і два нормальних вектора до неї. Видно, що лежать на одній прямій обидва вектора. Кут між ними становить 180 o.
Рівняння
Кут між двома площинами можна визначити, якщо відомо математичне рівняння розглянутого геометричного елемента. Існує кілька видів таких рівнянь, назви яких перераховані нижче:
- загального типу;
- векторне;
- у відрізках.
Ці три види є найбільш зручними при вирішенні різного роду задач, тому вони найчастіше використовуються.
Рівняння загального типу виглядає наступним чином:
A*x + B*y + C*z + D = 0.
Тут x, y, z – координати довільної точки, що належить даній площині. Параметри A, B, C і D представляють собою числа. Зручність цієї форми запису полягає в тому, що числа A, B, C є координатами нормальної до площини вектора.
Векторна форма запису площині може бути представлена наступним чином:
x, y, z) = (x0, y0, z0) + α*(a1, b1, c1) + β*(a2, b2, c2).
Тут (a2, b2, c2) і (a1, b1, c1) – параметри двох векторів, координати, які належать розглянутій площині. Точка (x0, y0, z0) також лежить в цій площині. Параметри α і β можуть приймати незалежні один від одного і довільні значення.
Нарешті, рівняння площини у відрізках представляють в наступному математичному вигляді:
x/p + y/q + z/l = 1.
Тут p, q, l – конкретні числа (в тому числі негативні). Цей вид рівняння зручний, коли необхідно зобразити в прямокутній системі координат площину, оскільки числа p, q, l показують точки перетину з осями x, y і z площині.
Зауважимо, що кожен вид рівняння може бути перетворений в будь-який інший за допомогою нескладних математичних операцій.