Призма є полиэдром або многогранником, який вивчають у шкільному курсі стереометрії. Одним з важливих властивостей цього багатогранника є його обсяг. Розглянемо в статті як можна обчислити цю величину, а також наведемо формули об’єму призм – правильних чотирикутної і шестикутної.
Призма в стереометрії
Під цією фігурою розуміють полиэдр, який складається з двох однакових багатокутників, розташованих у паралельних площинах, і з декількох паралелограмів. Для певних видів призм паралелограми можуть представляти прямокутні чотирикутники або квадрати. Нижче показаний приклад так званої п’ятикутної призми.
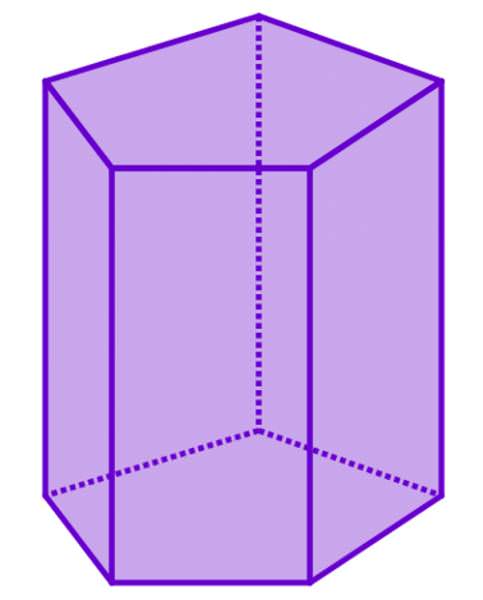
Щоб побудувати фігуру як на малюнку вище, необхідно взяти п’ятикутник і виконати його паралельний перенесення на деяку відстань в просторі. Поєднавши боку двох п’ятикутників з допомогою паралелограмів ми отримаємо шукану призму.
Всяка призма складається з граней, вершин і ребер. Вершини призми, на відміну від піраміди, є рівноправними, кожна з них відноситься до одного з двох підстав. Грані і ребра бувають двох типів: ті, що належать підстав, і ті, що відносяться до бічних сторін.
Призми бувають декількох видів (правильні, похилі, опуклі, прямі, увігнуті). Розглянемо далі в статті за якою формулою об’єм призми розраховується, беручи до уваги вигляд фігури.
Загальний вираз для визначення об’єму призми
Незалежно від того, до якого виду відноситься вивчається фігура, вона є прямою або похилої, правильної або неправильної, існує універсальне вираз, що дозволяє визначити її обсяг. Об’ємом просторової фігури називають область простору, яка укладена між гранями. Загальна формула об’єму призми виглядає так:
V = So × h.
Тут So являє собою площу основи. Слід запам’ятати, що мова йде саме про одній підставі, а не про двох. Величина h – це висота. Під висотою досліджуваної фігури розуміють відстань між її однаковими підставами. Якщо ця відстань збігається з довжинами бічних ребер, тоді говорять про прямий призми. У прямій фігури всі бокові сторони, є прямокутниками.
Таким чином, якщо призма є похилій і має неправильний багатокутник в основі, то розрахунок обсягу ускладнюється. Якщо ж фігура є прямою, то обчислення обсягу зводиться тільки до визначення площі підстави So.
Визначення обсягу правильної фігури
Правильною називається будь-яка призма, яка є прямою і має многоугольное основу з рівними один одному сторонами і кутами. Наприклад, такими правильними многокутниками є квадрат і рівносторонній трикутник. У той же час ромб не є правильною фігурою, оскільки не всі його кути рівні між собою.
Формула об’єму призми правильної однозначно випливає із загального виразу для V, яке було записано в попередньому пункті статті. Перш ніж переходити до запису відповідної формули, необхідно визначити площу правильного підстави. Не вдаючись у математичні подробиці, наведемо формулу визначення вказаної площі. Вона носить універсальний характер для будь-якого правильного n-кутника і має наступний вигляд:
Sn = n / 4 × ctg (pi / n) × a2.
Як видно з виразу, площа Sn – це функція двох параметрів. Ціле число n може приймати значення від 3 до нескінченності. Величина a – це довжина сторони n-кутника.
Для обчислення об’єму фігури необхідно лише помножити площу Sn на висоту h або на довжину бічного ребра b (h=b). В підсумку приходимо до наступної робочої формулою:
V = n / 4 × ctg (pi / n) × a2 × h.
Зауважимо, що для визначення об’єму призми довільного виду необхідно знати кілька величин (довжини сторін основи, висоту, двогранні кути фігури), для розрахунку ж величини V правильної призми нам слід знати лише два лінійних параметра, наприклад, a і h.
Обсяг призми правильної чотирикутної
Чотирикутна призма називається параллелепипедом. Якщо у неї всі грані рівні і являють собою квадрати, то така фігура буде кубом. Кожен школяр знає, що обсяг прямокутного паралелепіпеда або куба визначається в результаті множення трьох його різних сторін (довжини, висоти і ширини). Цей факт випливає з записаного загального вираження обсягу для правильної фігури:
V = n/4 × ctg (pi / n) × a2 × h = 4/4 × ctg ( pi / 4) × a2 × h = a2 × h.
Тут котангенс від 45° дорівнює 1. Зауважимо, що рівність висоти h і довжини сторони підстави a автоматично призводить до формули об’єму куба.
Обсяг призми правильної шестикутної
Тепер застосуємо викладену вище теорію для визначення об’єму фігури з шестикутним підставою. Для цього слід лише підставити значення n=6 в формулу:
V = 6/4 × ctg (pi / 6) × a2 × h = 3 × √3/2 × a2 × h.
Записане вираз можна отримати самостійно, не користуючись універсальною формулою для Sn. Щоб це зробити необхідно розділити правильний шестикутник на шість рівносторонніх трикутників. Сторона кожного з них буде дорівнює a. Площа одного трикутника відповідає:
S3 = √3/4 × a2.
Помноживши цю величину на кількість трикутників (6) і на висоту, ми отримаємо записану вище формулу для об’єму.
