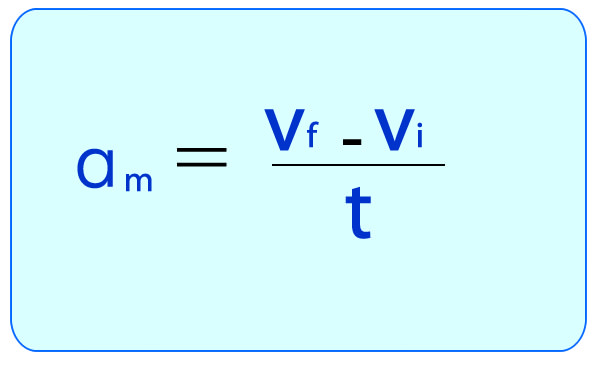
Як відомо, будь-яка фізична величина відноситься до одного з двох типів, вона є скалярною, або у векторній формі. У цій статті розглянемо такі кінематичні характеристики, як швидкість і прискорення, а також покажемо, куди спрямовані вектори прискорення і швидкості.
Що таке швидкість і прискорення?
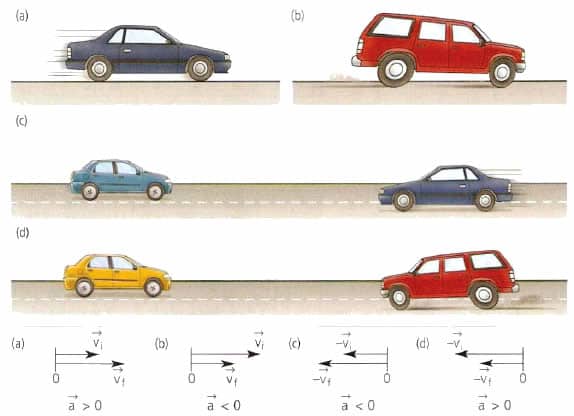
Обидві величини, названі у цьому пункті, є важливими характеристиками будь-якого руху, будь то переміщення тіла по прямій лінії або по криволінійній траєкторії.
Швидкістю називається швидкість зміни координат у часі. Математично ця величина дорівнює похідній за часом пройденого шляху, тобто:
v = dl/dt.
Тут вектор l спрямований від початкової точки шляху до кінцевої.
У свою чергу прискорення – це швидкість, з якою змінюється в часі сама швидкість. У вигляді формули це може бути записано так:
a = dv/dt.
Очевидно, що взявши другу похідну від вектора переміщення l за часом, ми також отримаємо значення прискорення.
Оскільки швидкість вимірюється в метрах в секунду, то прискорення, згідно записаного виразу, вимірюється в метрах на секунду в квадраті.