В геометрії при вивченні того чи іншого класу фігур наводять ряд формул, які дозволяють кількісно охарактеризувати аналізований об’єкт з різних сторін. У даній статті буде розглянуто фігура призма, і формули площі поверхні і об’єму для неї будуть наведені.
Що розуміють під призмою в стереометрії?
Коли говорять про призмі, то мають на увазі тривимірний многогранник, який утворений двома однаковими плоскими n-косинцями і n параллелограммами. Обидва n-кутника повинні обов’язково знаходитися в паралельних площинах, вони називаються сторонами підстав фігури. Що стосується паралелограмів, то вони утворюють бічну поверхню і можуть являти собою ромби, прямокутники і квадрати.
Як всякий багатогранник, призма складається з вершин, ребер і граней. Про межі ми вже згадали. Вершини призми, на відміну від вершин піраміди, є рівноправними і належать підстав. Ребра призми бувають двох видів: що належать підстав та належать до бічних гранях.
При формуванні конкретної назви призми в нього включають чотири типи класифікації. Ці типи простіше зрозуміти, якщо навести кілька прикладів.
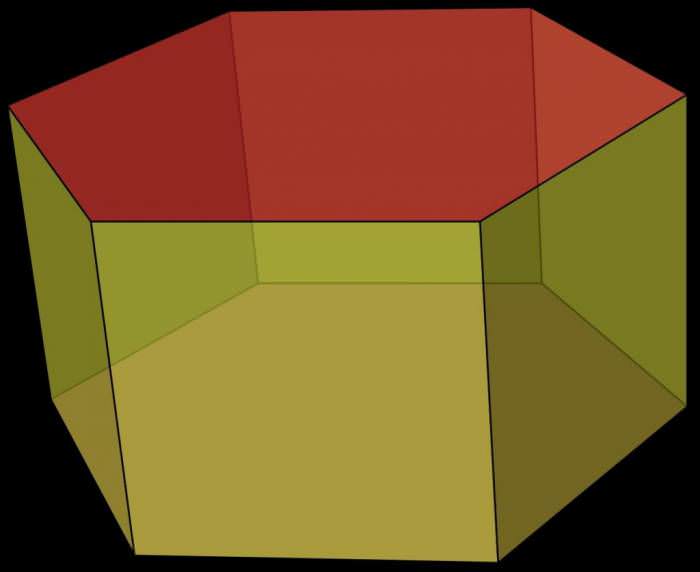
На малюнку вище показано шестикутна опукла правильна пряма фігура. Шестикутної і опуклою вона називається тому, що підставою її є опуклий шестикутник. Правильної і прямий фігура є тому, що сам шестикутник має рівні сторони і кути, а бічна поверхня представлена однаковими прямокутниками.
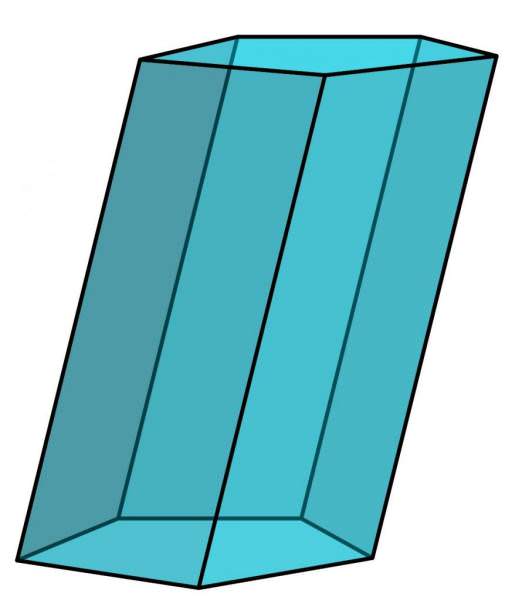
На цьому малюнку зображена п’ятикутна опукла неправильна похила призми. Пропонуємо читачеві самостійно розібратися, чому їй дано таку назву.
Лінійні і кутові параметри призм
Для довільної призми однозначне опис її характеристик вимагає знання лінійних параметрів і двогранних кутів між гранями. Головними лінійними параметрами є довжини сторін ai підстави, довжина бічного ребра b і висота h. Зауважимо, що сторони підстави можуть мати різні довжини, бічні ж ребра навіть в похилій фігурі дорівнюють один одному. Для прямої і правильної призм довжина бічного ребра b збігається з висотою h (b=h). Для обчислення висоти призми похилій необхідно знати значення двогранних кутів між площинами підстави і бічними параллелограммами.
Знання перелічених лінійних параметрів дозволяє обчислити площу поверхні фігури та її обсяг.
Поверхня фігури
Одними з важливих формул призми є вирази, які дозволяють обчислити її площу. Для визначення площі всіх граней фігури зручно розгорнути її на площині. Приклад однієї з розгорток наведено нижче.
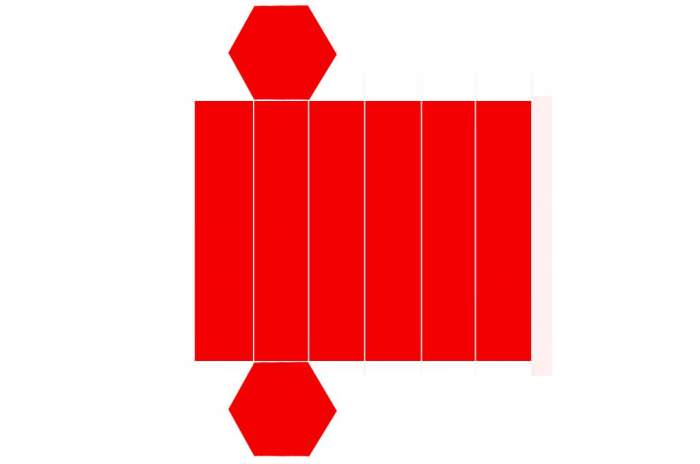
Для довільної призми формула площі всієї поверхні визначається так:
S = 2*So + Sb = 2*So + b*Psr
Де So – площа однієї підстави, Psr – периметр перпендикулярного всім бічним граням зрізу.
У разі правильної призми формула для S приймає вигляд:
S = n/2*ctg(pi/n)*a2 + n*a*h
Тут n – число вершин (сторін) багатокутника в підставі. Перший доданок тут відображає дві площі підстав, другий доданок – це сума площ всіх бічних прямокутників призми.
Наприклад, формула трикутної призми правильної прийме вигляд:
S3 = √3/2*a2 + 3*a*h
Відзначимо, що для визначення площі будь-якої правильної фігури досить знати дві її будь параметра. В даному випадку цими параметрами є сторона підстави a і висота h.
Формули для розрахунку обсягу
Під обсягом багатогранника розуміють частину простору, яка укладена між гранями. Для обчислення обсягу довільного виду призми необхідно скористатися тією ж самою формулою, що і для об’єму циліндра. Вона має наступний вигляд:
V = So*h
Незважаючи на простоту цього виразу, розрахунок може ускладнюватися тим, що спочатку потрібно обчислити висоту і площу основи. Для похилої призми з неправильним опуклим або увігнутим підставою ця задача не є тривіальною і не має спільного рішення. В такому разі слід скористатися загальним підходом: знаючи двогранний кут при основі і одну з діагоналей підстави або бічне ребро, можна обчислити висоту фігури; площа багатокутного підстави складається з площ елементарних фігур, формули для яких відомі.
Якщо вивчається призма є правильною, тоді для неї можна записати конкретне вираження. Формула об’єму призми правильної приймає вигляд:
V = n/4*ctg(pi/n)*a2*h

Наприклад, для трикутної фігури отримуємо:
V3 = √3/4*a2*h
Як і для площі S, для визначення обсягу V правильної фігури необхідно знати висоту і сторону основи.












