Кожен школяр знає, що таке коло і якими параметрами вона характеризується. Рух по круговій траєкторії є одним з найпоширеніших у природі видів переміщення об’єктів. Що це – рівномірний рух по колу, і якими формулами воно описується, розповімо в даній статті.
Рух обертання

Щоб краще зрозуміти, про що йде мова, відразу наведемо приклади цього виду переміщення тіл у просторі. Прикладами є:
- обертання металевого валу;
- рух колеса автомобіля або велосипеда;
- розкручування каменю, прив’язаний до мотузки;
- обертання іграшки-дзиги;
- рух нашої планети навколо Сонця і навколо власної осі.
Елементами, які характеризують розглянутий вид руху, є:
- Окружність, яка володіє деяким радіусом r. Окружність є траєкторією руху.
- Вісь, навколо якої відбувається обертання. Вона розташована в центрі кола в площині перпендикулярній їй.
У фізиці для опису будь-якого переміщення об’єктів застосовують набір кінематичних величин. Далі наведемо ці величини для обертального руху.
Кутові характеристики обертання
До них відносяться кут повороту θ, кутова швидкість ω і кутове прискорення α. У фізиці рівномірного руху по колу ці три величини приймають певне значення.
Що стосується кута θ, то його фізичний зміст інтуїтивно зрозумілий. Величина θ показує центральний кут кругового сектора, на який тіло повертається за відомий проміжок часу. Далі у формулах його виражають в радіанах. Нагадаємо, що повна окружність відповідає 2*pi радианам.
Швидкість ω є аналогом лінійної величини, тільки її одиницями виміру є радіан за секунду. В диференціальній формі математичне визначення величини ω виглядає так:
ω = dθ/dt
Кутова швидкість показує швидкість обертання тіла. Її можна використовувати для розрахунку частоти обертання f в оборотах в секунду. Для цього використовують формулу:
f = ω/(2*pi)
Прискорення α показує, як швидко змінюється швидкість обертання ω. Тобто для нього справедливо вираз:
α = dω/dt
Одиницею вимірювання величини α є радіани в квадратну секунду (рад/с2).
Що це – рівномірний рух по колу?
Фізики 10 класу детально вивчають розглянуту тему. Кожен знає, що прямолінійний рух буде рівномірним, якщо лінійна швидкість v тіла залишається постійною. У випадку обертального руху можна дати наступне визначення: рівномірний рух по колу – це обертання тіла з постійною кутовою швидкістю. Оскільки остання не змінюється, то кутове прискорення α дорівнює нулю. Наведені міркування дозволяють записати основну формулу, що описує розглянутий вид переміщення тіл:
θ = ω*t
У виразі ω = const, а величини θ t змінюються. Графічним представленням цього типу руху є пряма лінія, яка проходить через початок координат. Тангенс кута між цією лінією і віссю x дорівнює модулю кутової швидкості ω.
Особливість рівномірного руху по колу – це проходження тілом за однакові проміжки часу однакових кутових відрізків. Ця особливість відрізняє рівномірне обертання від прискореного.
Лінійна і кутова швидкість при рівномірному русі по колу
До теперішнього часу кінематика обертального руху розглядалася в рамках кутових характеристик. Їх використання є зручним для рішення практичних завдань. Тим не менше іноді виявляється корисним знати лінійні характеристики обертової системи. Найважливішою з них є лінійна швидкість v.
Щоб знайти зв’язок між величинами v, ω, припустимо, що обертання матеріальної точки здійснюється по колу радіусом r. Тоді лінійна швидкість при рівномірному русі по колу – це величина, яка розраховується за формулою:
v = 2*pi*r/t
Де t – час вчинення тілом одного оберту навколо осі обертання. Кутова швидкість ω при цьому може бути розрахована так:
ω = 2*pi/t
Порівнюючи ці вирази, приходимо до формули:
v = ω*r
Таким чином, лінійна швидкість матеріальної точки, що обертається по коловій траєкторії з радіусом r, є величиною постійною. Однак якщо розглядається обертання масивного тіла, то лінійна швидкість кожної його точки буде зростати зі збільшенням відстані до осі обертання, а величина ω при цьому залишається постійною.
Центростремительное прискорення
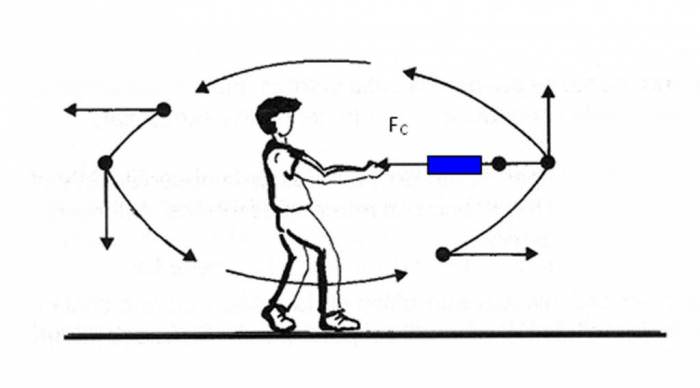
Щоб тіло мало можливість обертатися по колу, необхідно присутність деякої сили, яка по відношенню до обертовою системі є внутрішньою. Ця сила забезпечує викривлення прямолінійної траєкторії руху будь-якого тіла, що володіє інерційними властивостями. Мова йде про доцентровою силою, яка спрямована від центру мас тіла до осі обертання. Рівномірний рух по колу і центростремительное рух – це один і той же процес. Якщо б не було доцентрової сили, то обертання було б неможливо.
Згідно із законами Ньютона, дія на тіло сили призводить до появи прискорення. При рівномірному русі по колу не існує кутового прискорення (воно дорівнює нулю), однак існує центростремительное прискорення. Його розраховують за формулою:
ac = v2/r
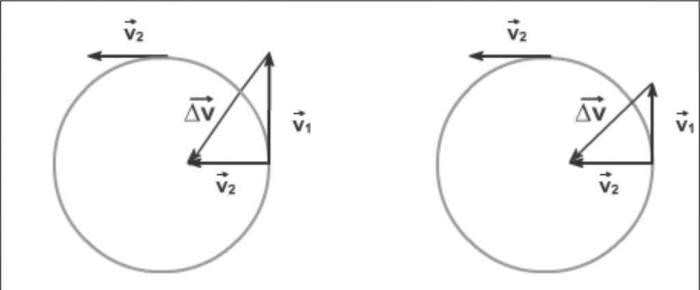
Прискорення ac не призводить до зміни модуля швидкостей v і ω. Результатом його дії є зміна напрямку вектора v.
Рішення завдання
Вважаючи рух нашої планети навколо Сонця рівномірним, необхідно знайти значення доцентрового прискорення, з яким сонячна гравітація діє на Землю.

Через кутову швидкість можна записати наступну формулу для ac:
ac = ω2*r
У свою чергу величина ω для Землі визначається за формулою:
ω = 2*pi/T
Тоді отримуємо для доцентрового прискорення ac:
ac = 4*pi2*r/T2
Де r – середня відстань від землі до світила, T – земний рік. Враховуючи, що r = 149,6 млн км, T = 365,3 дня, отримуємо відповідь: ac = 0,006 м/с2. Ця величина в сотні разів менше типових лінійних прискорень при русі транспортних засобів.