Однією з цікавих і практично важливих тем у фізиці є термодинаміка газів. Системи, що знаходяться в цьому агрегатному стані, розглядають з використанням так званої моделі ідеального газу. Дана стаття присвячена вивчаються у 10 класі изопроцессам у фізиці та вирішення задач на цю тему.
Модель ідеального газу і рівняння стану
Як відомо, гази являють собою високоенергетичні системи, які здатні легко змінювати свою форму і об’єм. Модель ідеального газу полягає в тому, що вона передбачає відсутність розмірів у частинок і взаємодії між ними. Справедливість цієї моделі очевидна в ряді практичних випадків, оскільки відстані між газовими молекулами набагато перевищують їх лінійні розміри, а кінетична енергія їх руху на кілька порядків більше слабких взаємодій між хімічно нейтральними частками.
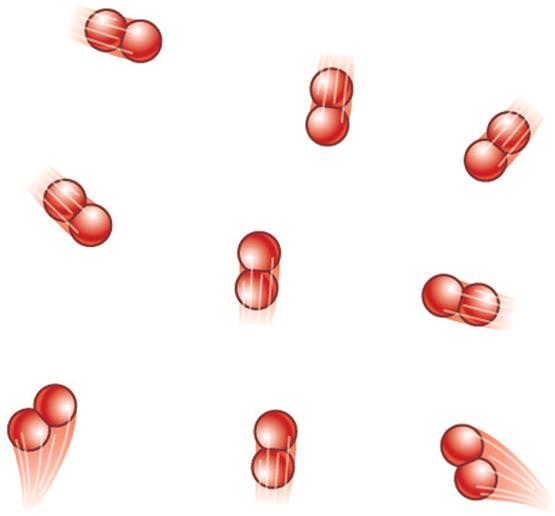
В 30-е роки XIX століття, збираючи та аналізуючи весь наявний експериментальний матеріал, французький вчений Клапейрона записав універсальне рівняння, що описує стан будь ідеальної газової системи. Це рівняння має вигляд:
P*V = n*R*T.
Видно, що в рівності містяться всі три основні термодинамічні змінні (P – тиск, V – об’єм і T – температура). Крім того, воно не залежить від хімічних властивостей системи, а визначається лише кількістю речовини n в ній. Символом R позначена газова постійна, рівна 8,314 Дж/(моль*К).
Ізотермічний процес
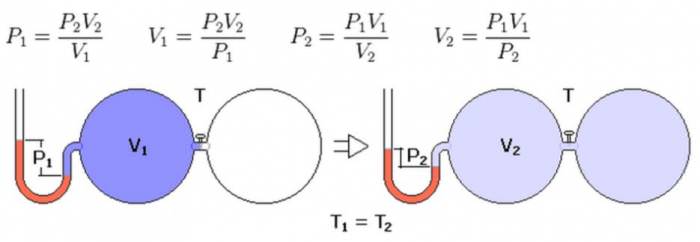
Почнемо вивчати изопроцессы у фізиці з розгляду переходу системи між двома рівноважними станами при постійній температурі. Якщо система є закритою, тобто, вона може обмінюватися теплом з навколишнім середовищем, але не з речовиною, то права частина рівності у наведеному вище рівнянні стану буде постійною величиною. Цей факт призводить до наступного изотермическому законом:
P*V = const при T=const.
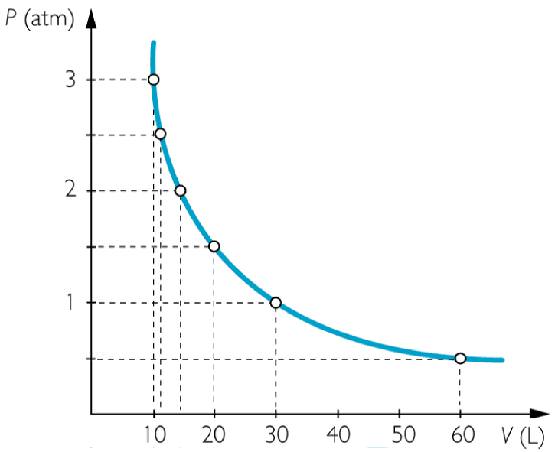
Ця рівність називається законом Бойля-Маріотта у честь прізвищ учених, які вперше виявили його експериментально в XVII столітті. Якщо зобразити изотерму в осях P та V, то вона буде представляти собою гіперболу, показану нижче на малюнку.
Приклад завдання на закон Бойля-Маріотта
Вирішимо таку просту задачу з фізики на изопроцессы (10 клас):
Відомо, що газ під поршнем розширюється ізотермічно. Чому буде дорівнювати кінцевий тиск в системі, якщо на початку воно складало одну атмосферу? Обсяг в результаті розширення газу збільшився в 3 рази.
Запишемо закон Бойля-Маріотта у такому вигляді:
P1*V1 = P2*V2.
Перетворимо цю рівність таким чином, щоб однакові фізичні величини опинилися в одній частині рівності:
P2/P1 = V1/V2.
Звідки отримуємо кінцевий вираз для P2 і відповідь на запитання задачі:
P2 = P1*V1/V2 = 1*1/3 = 0,33 атм.
Кінцевий тиск в системі в 3 рази менше початкової.
Ізобарний процеси і ізохорний
Обидва процеси були спеціально винесені в один пункт статті, оскільки вони описуються математичними виразами однієї форми.
Якщо газова система розширюється або стискається, зберігаючи постійний тиск, то говорять про изобарном процесі. В такому випадку користуються наступною формулою:
V/T = const при P = const.
Цей вираз може бути отримано з рівняння стану. Воно називається законом Шарля (прізвище француза, який відкрив закон в кінці XVIII століття).
Тепер припустимо, що ми почали нагрівати газ у твердому закритій посудині. Обсяг при цьому буде залишатися постійним. Що буде відбуватися з температурою і тиском в системі? Експерименти і рівняння стану кажуть, що ці величини будуть рости пропорційно один одному, тобто:
P/T = const при V = const.
Описаний процес називається изохорным, а закон, що відображає його, названий на честь француза Гей-Люссака, який першим вивчив експериментально і опублікував на початку XIX століття.
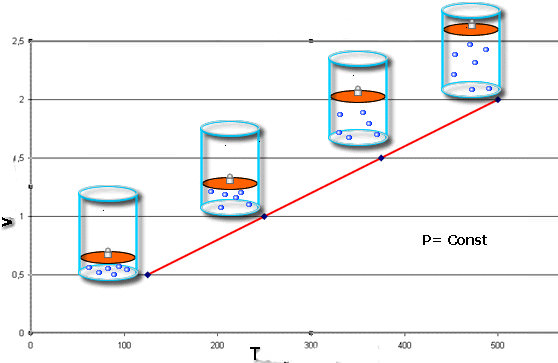
З наведених формул випливає, що їх графічне зображення в осях V-T (изобар) і P-T (изохора) являє собою прямолінійну залежність. Приклад ізобари показаний нижче.
Приклад завдання на закон Шарля
Розглянемо наступну задачу з фізики на изопроцессы:
В одному циліндрі під рухомим поршнем міститься 2 міль деякого газу при тиску 1 атмосфера. В іншому циліндрі знаходиться газ в кількості речовини 3 моль, тиск в ньому становить 1,5 атмосфери. Обидва циліндра почали нагрівати при постійному тиску. Як будуть взаємно розташовані изобарные лінії на графіку в осях V-T для процесів в кожному циліндрі?
Щоб відповісти на поставлене питання, слід записати закон Шарля у такому вигляді:
V = const*T.
Це означає, що тангенс кута нахилу для кожної прямої дорівнює величині константи. Якщо її знайти для процесів в кожному циліндрі, то ми отримаємо відповідь на завдання. Для цього скористаємося рівнянням стану, маємо:
P*V = n*R*T =>
V/T = n*R/P.
Права частина останньої рівності є тією константою, яку ми шукаємо. Як видно, вона залежить прямо пропорційно від кількості в системі речовини і обернено пропорційно від тиску. Підставляючи ці величини з умови, отримаємо значення констант для кожного процесу:
const1 = n1*R/P1 = 2/1*R = 2*R;
const2 = n2*R/P2 = 3/1,5*R = 2*R.
Таким чином, значення констант для обох процесів рівні, що означає повне збіг графіків изобар. Зауважимо, що при обчисленні констант ми підставляли тиск в атмосферах. Рівність const1 і const2 не зміниться, якщо підставити тиску в паскалях.
Приклад завдання на закон Гей-Люссака
Як було показано, успішне вирішення завдань з фізики на изопроцессы вимагає знання не тільки самих процесів, але й уміння використовувати для них рівняння стану. Наведемо приклад ще однієї подібної задачі.
Кисень масою 20 грамів знаходиться в закритій посудині об’ємом 2 літра. Охолодження судини на 10 градусів Цельсія призвело падіння тиску в посудині на деяку величину. Необхідно визначити кінцеве рівноважний тиск в системі, якщо на початку воно було дорівнює одній атмосфері.
У задачі мова йде про изохорном переході газоподібного кисню. Отримаємо робочу формулу для нього. Для цього виразимо відношення тиску до температури з рівняння стану:
P/T = n*R/V = m*R/(M*V).
Де кількість речовини n записано як відношення маси газу m до його молярної маси M. Користуючись цим виразом, визначимо різницю між кінцевим і початковим тисками, отримуємо:
P2 – P1 = m*R/(M*V)*(T2 – T1).
Звідки приходимо до кінцевого висловом, дозволяє відповісти на поставлене в задачі запитання:
P2 = P1 + m*R/(M*V)*T, де T = T2 – T1.
Підставляти всі відомі величини в формулу слід в одиницях СІ. Після підстановки і проведення обчислень, приходимо до відповіді: P2 = 75343,75 Па, що дорівнює тиску в 0,74 атмосфери.












