Просторові фігури докладно розглядаються в старших класах загальноосвітніх шкіл у курсі стереометрії. Дана стаття містить відповідь на питання про те, як знайти твірну конуса круглого прямого і утворить відповідної усіченої фігури.
Фігура конус
Щоб зрозуміти, як знайти твірну конуса, слід дати уявлення про цю постать. Круглим прямим конусом називають фігуру обертання прямокутного трикутника навколо одного з катетів. Малюнок нижче демонструє процес обертання.
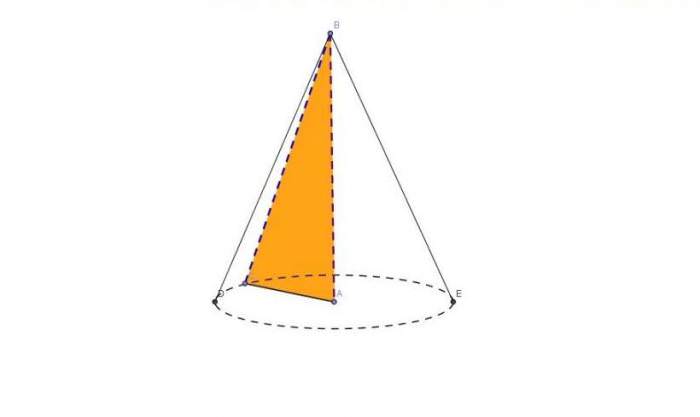
Отримана просторова фігура має такі характеристики:
Зауважимо, що висота фігури перетинає кругле підставу в його центрі. Це є достатньою умовою, щоб вважати конус прямим.
Твірна конуса
Тепер можна переходити до відповіді на питання про те, як знайти твірну конуса круглого прямого. Вище було сказано, що вона представляє собою відрізок, який лежить на конічній поверхні і з’єднує вершину з точкою окружності підстави. В прямокутному трикутнику, з якого був конус отримано, що утворює є гіпотенузою. Це спостереження дозволяє записати відому теорему Піфагора, зв’язавши утворить g з радіусом r і висотою h фігури. Формула, як знайти твірну конуса, має вигляд:
g = √(r2 + h2)
Крім цієї формули, на практиці замість висоти або радіусу фігури може бути відомий кут φ між твірною і підставою. У цьому випадку генератрису g можна розрахувати за допомогою наступних виразів:
g = h/sin(φ);
g = r/cos(φ)
Ці формули випливають з властивостей тригонометричних функцій синуса і косинуса.
Таким чином, обчислення твірної конуса можливо, якщо знати будь-які два параметри фігури.
Фігура усічений конус
Він також є фігурою обертання, тільки замість прямокутного трикутника слід обертати прямокутну трапецію. На малюнку нижче показаний усічений конус.
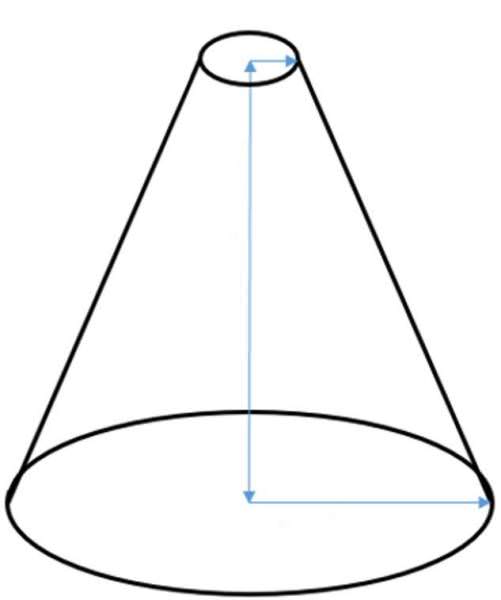
Тут сині стрілки показують прямокутну трапецію. Довжина вертикальної стрілки є висотою h фігури, довжини двох інших синіх стрілок – це радіуси підстав конуса. На відміну від циліндра, підстави усіченого конуса мають різну площу. Позначимо їх радіуси r1 і r2. Четверта похила до основи сторона трапеції є твірною або генератрисой. Як і для звичайного конуса, для усіченого всі генератрисы дорівнюють одна одній і утворюють бічну поверхню фігури.
Зауважимо, що усічений конус отримав таку назву тому, що його можна одержати не тільки обертанням трапеції, але і за допомогою відсікання площиною верхній частині круглого прямого конуса.
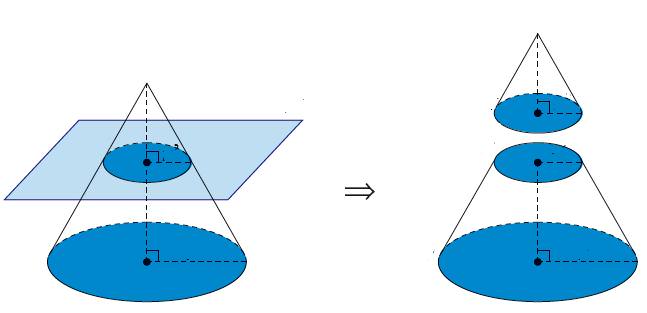
Генератриса усіченої фігури
Отже, ми познайомилися з усіченим конусом, а також з поняттям про його утворює. Як знаходити утворить усіченого конуса? Для того щоб одержати потрібну формулу, зауважимо, якщо висоту h перенести паралельно самій собі до бічної поверхні конуса так, щоб вона стосувалася одним кінцем утворює фігури, то вийде прямокутний трикутник. Його сторонами будуть висота h (катет), генератриса g (гіпотенуза) і r1-r2 (катет). Тоді можна записати формулу для визначення g:
g = √((r1 – r2)2 + h2)
Відповідно, якщо дано гострий кут φ1 між великим підставою і генератрисой, тоді останню можна визначити так:
g = h/sin(φ1);
g = (r1 – r2)/cos(φ1)
Якщо ж відомий тупий кут φ2 між малим підставою і генератрисой, тоді для її обчислення необхідно застосовувати такі вирази:
g = h/sin(φ2);
g = (r2 – r1)/cos(φ2)
Тут перша формула є точно такою ж, як для кута φ1, а в другій формулі радіуси в чисельнику помінялися місцями.
Таким чином, знайти твірну конуса усіченого можна, якщо знати будь-які три його параметра.












