Дослідження функцій та їх графіків – це тема, якій приділяється особлива увага в рамках шкільної програми для старших класів. Деякі основи математичного аналізу – диференціювання – включені в профільний рівень іспиту з математики. У деяких школярів виникають проблеми з цією темою, так як вони плутають графіки функції та похідної, а також забувають алгоритми. У цій статті будуть розглянуті основні типи завдань та способи їх вирішення.
Що таке значення функції?
Математична функція являє собою особливу рівняння. Воно встановлює взаємозв’язок між числами. Функція залежить від значення аргументу.
Значення функції розраховується по заданій формулі. Для цього слід підставити будь-який аргумент, який відповідає області допустимих значень, в цю формулу на місце х і виконати необхідні математичні операції. Які?
Як можна знайти найменше значення функції, використовуючи графік функції?
Графічне зображення залежності функції від аргументу називається графіком функції. Він будується на площині з певним одиничним відрізком, де по горизонтальній осі абсцис відкладається значення змінною, або аргументом, а по вертикальній осі ординат – відповідне йому значення функції.

Чим більше значення, тим правіше він лежить на графіку. І чим більше значення самої функції, тим вище знаходиться точка.
Про що це говорить? Найменшим значенням функції буде точка, яка лежить нижче всього на графіку. Для того щоб знайти його на відрізку графіка, потрібно:
1) Знайти і відзначити кінці цього відрізка.
2) Візуально визначити, яка точка на цьому відрізку лежить нижче всього.
3) У відповідь записати її числове значення, яке можна визначити, спроектувавши точку на вісь ординат.
Точки екстремуму на графіку похідної. Де шукати?
Однак при вирішенні завдань іноді даний графік не функції, а її похідною. Для того, щоб випадково не допустити дурну помилку, краще уважно читати умови, так як від цього залежить, де потрібно шукати точки екстремуму.

Отже, похідна – це миттєва швидкість зростання функції. Згідно геометричного визначення похідна відповідає кутовому коефіцієнту дотичної, яка безпосередньо проведена до даної точки.
Відомо, що в точках екстремуму дотична паралельна осі Ox. Це означає, що її кутовий коефіцієнт – 0.
З цього можна зробити висновок, що в точках екстремуму похідна лежить на осі абсцис або звертається в нуль. Але крім того, в цих точках функція змінює свій напрямок. Тобто після періоду зростання починає спадати, а похідна, відповідно, змінюється з позитивної на негативну. Або навпаки.
Якщо похідна з позитивною стає негативною – це точка максимуму. Якщо з негативною стає позитивною – точка мінімуму.
Важливо: якщо у завданні потрібно вказати точку мінімуму або максимуму, то у відповідь слід записати відповідне значення по осі абсцис. Але у випадку, якщо потрібно знайти значення функції, то попередньо потрібно підставити відповідне значення аргументу функції і розрахувати його.
Як знаходити точки екстремуму функції за допомогою похідної?
Розглянуті приклади в основному відносяться до завдання під номером 7 іспиту, який передбачає роботу з графіком похідної або первісної. А ось завдання 12 ЄДІ – знайти найменше значення функції на відрізку (іноді – найбільша) – виконується без будь-яких креслень і вимагає базових навичок математичного аналізу.
Для його виконання потрібно вміти знаходити точки екстремуму функції за допомогою похідної. Алгоритм їх знаходження такий:
- Знайти похідну від функції.
- Прирівняти її до нуля.
- Знайти корені рівняння.
- Перевірити, чи є отримані точки точками екстремуму або перегину.
Для цього потрібно накреслити схему і на одержані проміжках визначити знаки похідної, підставляючи числа, що належать відрізкам, в похідну. Якщо при рішенні рівняння ви отримали коріння подвійний кратності – це точки перегину.
- Застосувавши теорему, визначити, які точки є точками мінімуму, а які – максимуму.
Обчислення найменшого значення функції з застосуванням похідної
Однак, виконавши всі ці дії, ми знайдемо значення точок мінімуму і максимуму по осі абсцис. Але як знайти найменше значення функції на відрізку?
Що необхідно зробити для того, щоб знайти число, якому відповідає функція в конкретній точці? Потрібно підставити в цю формулу значення аргументу.
Точки мінімуму і максимуму відповідають найменшим та найбільшим значенням функції на відрізку. Значить, щоб знайти значення функції, потрібно розрахувати функцію, використовуючи отримані значення х.
Важливо! Якщо в завданні потрібно вказати точку мінімуму або максимуму, то у відповідь слід записати відповідне значення по осі абсцис. Але у випадку, якщо потрібно знайти значення функції, то попередньо слід підставити відповідне значення аргументу функції і виконати необхідні математичні операції.
Що робити, якщо на даному відрізку відсутні точки мінімуму?
Але як знайти найменше значення функції на відрізку, на якому відсутні точки екстремуму?
Це означає, що на ньому функція монотонно спадає чи зростає. Тоді в функцію потрібно підставити значення крайніх точок цього відрізка. Є два шляхи.
1) Розрахувавши похідну і проміжки, на яких вона позитивна чи негативна, зробити висновок про те, убуває функція на даному відрізку або зростає.
Згідно з ними підставити функції більше або менше значення аргументу.
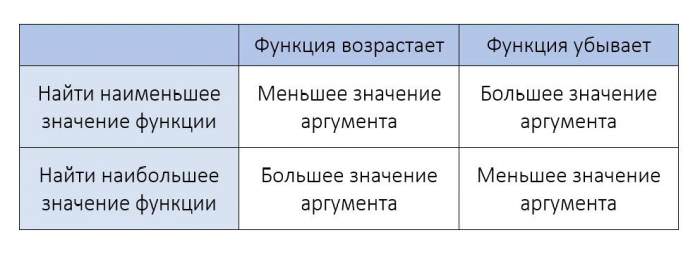
2) Просто підставити в функцію обидві точки і порівняти отримані значення функції.
В яких завданнях знаходження похідної необов’язково
Як правило, у завданнях ЄДІ все ж потрібно знаходити похідну. Є тільки пара винятків.
1) Парабола.

Вершина параболи знаходиться за формулою.
Якщо a < 0, то гілки параболи спрямовані вниз. Її вершина є точкою максимуму.
Якщо a > 0 гілки параболи спрямовані вгору, вершина – точка мінімуму.
Розрахувавши точку вершини параболи, слід підставити її значення у функцію і обчислити відповідне значення функції.
2) Функція y = tg x. Або y = ctg x.
Ці функції є монотонно зростаючими. Тому, чим більше значення, тим більше значення самої функції. Далі ми розглянемо, як знайти найбільше і найменше значення функції на відрізку з прикладами.
Основні типи завдань
Завдання: найбільше або найменше значення функції. Приклад на графіку.
На малюнку ви бачите графік похідної функції f (x) на інтервалі [-6; 6]. В якій точці відрізку [-3; 3] f (x) приймає найменше значення?
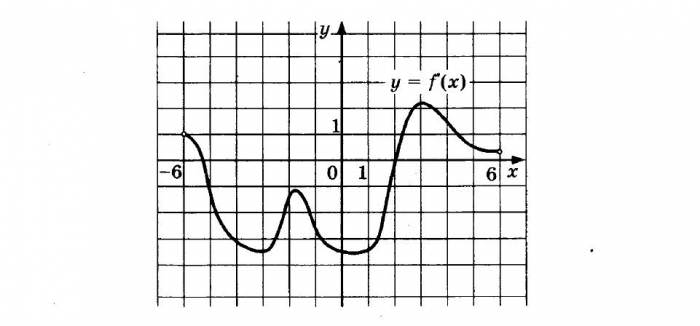
Отже, для початку слід виділити зазначений відрізок. На ньому функція один раз приймає нульове значення і змінює свій знак – це точка екстремуму. Так як похідна з негативною стає позитивною, значить, це точка мінімуму функції. Цій точці відповідає значення аргументу 2.
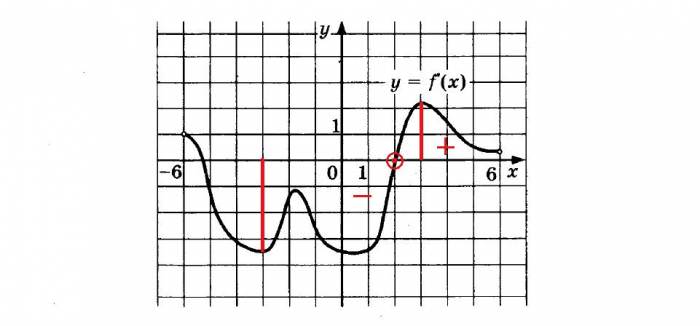
Відповідь: 2.
Продовжуємо розглядати приклади. Завдання: знайти найбільше і найменше значення функції на відрізку.
Знайдіть найменше значення функції y = (x – 8) ex-7 на відрізку [6; 8].
1. Взяти похідну від складної функції.
y’ (x) = (x – 8) ex-7 = (x – 8)’ (ex-7) + (x – 8) (ex-7)’ = 1 * (ex-7) + (x – 8) (ex-7) = (1 + x – 8) (ex-7) = (x – 7) (ex-7)
2. Порівняти одержану похідну до нуля і вирішити рівняння.
y’ (x) = 0
(x – 7) (ex-7) = 0
x – 7 = 0, або ex-7 = 0
x = 7; ex-7 ≠ 0, немає коренів
3. Підставити в функцію значення крайніх точок, а також отримані корені рівняння.
y (6) = (6 – 8) e6-7 = -2e-1
y (7) = (7 – 8) e7-7 = -1 * e0 = -1 * 1 = -1
y (8) = (8 – 8) e8-7 = 0 * e1 = 0
Відповідь: -1.
Отже, в цій статті була розглянута основна теорія про те, як знайти найменше значення функції на відрізку, необхідна для успішного вирішення завдань ЄДІ з математики профільної. Елементи математичного аналізу застосовуються при вирішенні завдань з частини іспиту, але очевидно, вони являють інший рівень складності, та алгоритми їх рішень складно вмістити в рамки одного матеріалу.