У цій статті розглянемо, як розраховувати площа правильної піраміди. Геометричні властивості фігур у просторі вивчає стереометрія. Цей розділ геометрії використовує поняття довжин відрізків і кутів між ними для визначення таких характеристик фігур, як площа або об’єм.
Що це за фігура?
Перш ніж переходити до розгляду конкретних формул площі правильної піраміди (бічна поверхні і підстави), слід пояснити, що вона являє собою з точки зору геометрії. Пояснимо.
Пірамідою називають будь-який геометричний об’єкт в просторі, який утворений в результаті з’єднання однієї точки з усіма вершинами деякого багатокутника. Так утворюється фігура. Загальна точка називається вершиною і площини многокутника не належить.
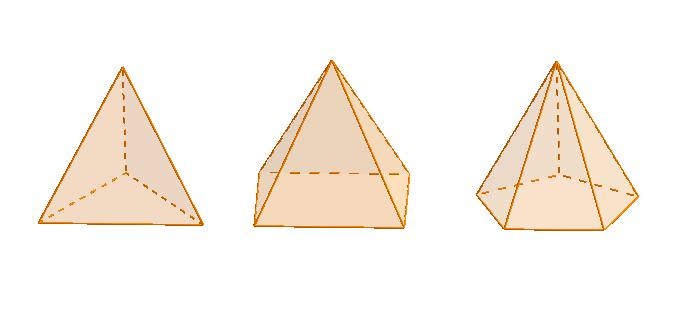
Вище показано три різних піраміди. Видно, що вони відрізняються кількістю сторін багатокутного підстави (три, чотири і п’ять). Проте всі ці фігури об’єднує те, що їх бічна поверхня складається з трикутників. Кількість їх різне, воно дорівнює числу сторін підстави.
З малюнка видно, що будь-яка піраміда складається з ребер, вершин і граней. Їх сукупність утворює єдиний об’єкт. Якщо з його вершини (точка перетину бічних трикутників) опустити перпендикуляр до основи, то його довжина буде заввишки фігури. Якщо цей відрізок закінчується в центрі підстави, то така піраміда буде називатися прямій. З цим розібралися, йдемо далі.
Пряма піраміда, основа якої є рівностороннім і рівнокутним гратки, називається правильною. Наведемо приклад. Піраміда Хеопса – це правильна чотирикутна фігура, оскільки вона є прямою і має квадратну основу.
Формули для визначення значень
У стереометрії для вивчення площі правильної піраміди і інших об’ємних фігур використовують їх розгортки. Пояснимо графічно. На малюнку показано, що являє собою розгортка правильної чотирикутної піраміди. Тепер стає більш зрозуміло, як проводити розрахунки.
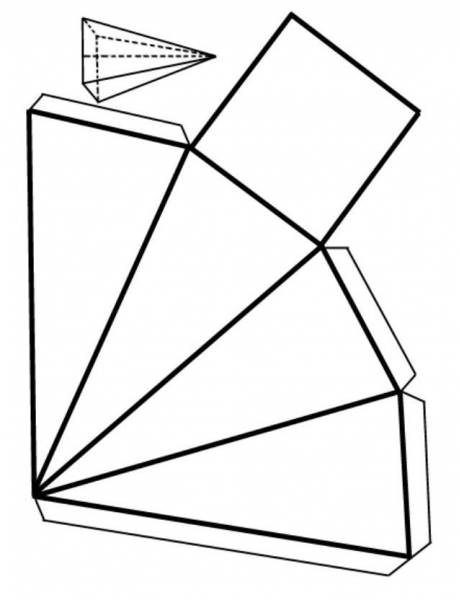
Видно, що площа правильної піраміди має дві складові: заснування і бічну поверхню. Присвоїмо змінні.
Позначимо площу основи символом So. Для обчислення цієї величини існує універсальна формула для правильного n-кутника. Вона має вигляд:
Sn = n / 4 * a2 * ctg (pi/n).
Тут n – кількість сторін підстави, a – сторона n-кутника.
У правильній піраміді всі трикутники, які утворюють бічну поверхню, рівні між собою і в загальному випадку є равнобедренными. Це означає, що для визначення фігури площі бічної поверхні (позначимо її Sb) необхідно знайти цей параметр у одного трикутника, а потім помножити на їх кількість. Запишемо формулу. Площа бічної сторони правильної піраміди розраховується так:
Sb1 = 1 / 2 * a * hb.
Тут hb – це висота трикутника, яка називається апофемой піраміди .
Оскільки кількість трикутників дорівнює числу сторін n-вугільного підстави, то отримуємо формулу для обчислення величини Sb:
Sb = n * Sb1 = n * a * hb / 2.
Тоді загальну площу правильної піраміди можна обчислити за формулою:
S = So + Sb = n / 4 * a2 * ctg(pi/n) + n * a * hb / 2.
Рішення завдання
Умова. Відомо, що правильна чотирикутна піраміда має довжину сторони основи 10 см і висоту 12 див. Чому дорівнює площа її поверхні?
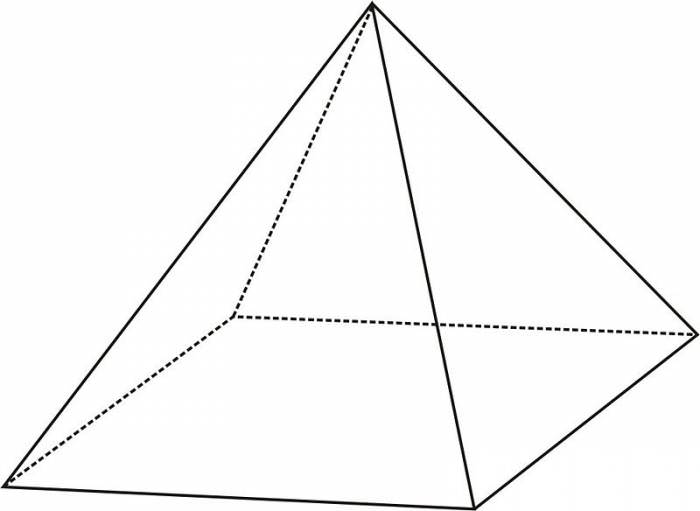
Рішення. Площа поверхні основи (квадрата) дорівнює:
So = a2 = 100 см2.
Щоб обчислити площу бічної поверхні , необхідно знати апофему hb фігури. Якщо розглянути прямокутний трикутник всередині піраміди, то апофема, що є в ньому гіпотенузою, обчислюється так:
hb = √(a2 / 4 + h2) = 13 див.
Тоді площа бічної поверхні правильної піраміди дорівнює:
Sb = n * a * hb / 2 = 4 * 10 * 13 / 2 = 260 см2.
Складаючи отримані значення So і Sb, приходимо до відповіді на питання завдання: S = 360 см2.
У статті розглянуто, як знайти площу фігури, званої правильної пірамідою.