Світ, який нас оточує, знаходиться в постійному русі. Тим не менше, існують системи, які можуть перебувати у відносному стані спокою та рівноваги. Однією з них є важіль. У цій статті розглянемо, що він собою представляє з точки зору фізики, а також вирішимо кілька завдань на умову рівноваги важеля.
Що таке важіль?
У фізиці називається важелем простий механізм, що складається з невагомою балки (дошки) і однієї опори. Розташування опори не є фіксованим, тому вона може знаходитися ближче до одного з кінців балки.
Будучи простим механізмом, важіль служить для перетворення сили в шлях, і навпаки. Незважаючи на те, що сила і шлях – це абсолютно різні фізичні величини, вони пов’язані один з одним формулою роботи. Щоб підняти який-небудь вантаж, необхідно зробити деяку роботу. Зробити це можна двома різними способами: додати велику силу і перемістити вантаж на невелику відстань або ж подіяти незначною силою, але при цьому збільшити шлях переміщення. Власне, для цього і служить важіль. Кажучи коротко, цей механізм дозволяє виграти в дорозі і програти в силі або, навпаки, виграти в силі, але програти в дорозі.

Діють на важіль сили
Дана стаття присвячена умов рівноваги важеля. Будь рівновагу в статиці (розділ фізики, що вивчає тіла в спокої) припускає наявність або відсутність сил. Якщо розглядати важіль у вільному вигляді (легка балка і опора), то на нього не діють ніякі сили, і він буде перебувати в рівновазі.
Коли з допомогою важеля будь-якого типу виконують роботу, то на нього завжди діють три сили. Перерахуємо їх:
- Вага вантажу. Оскільки розглянутий механізм служить для підйому вантажів, очевидно, що їх вага доведеться долати.
- Зовнішня сила протидії. Це та сила, яку прикладає людина або інша машина, щоб протидіяти вагою вантажу на балці важеля.
- Реакція опори. Напрям цієї сили завжди перпендикулярно площини балки важеля. Сила реакції опори спрямована вгору.
Умова рівноваги важеля передбачає розгляд не стільки зазначених діючих сил, скільки моментів сил, що створюються ними.
Що таке момент сили
У фізиці моментом сили, або обертовим моментом, називають величину, що дорівнює добутку зовнішньої сили на плече. Плечем сили називають відстань від точки прикладання сили до осі обертання. Наявність останньої є важливим при розрахунку моменту сили. Без наявності осі обертання немає ніякого сенсу говорити про момент сили. Враховуючи наведене визначення, можна записати наступний вираз для обертаючого моменту M:
M = F*d
Справедливості заради відзначимо, що момент сили в дійсності – це векторна величина, тим не менш для розуміння теми даної статті досить знати, як розраховується модуль моменту сили.
Крім формули вище, слід запам’ятати, що якщо сила F прагне повернути систему так, що та починає рух проти годинникової стрілки, то створюваний момент вважається позитивним. Навпаки, прагнення повернути систему по ходу стрілки годинника свідчить про негативний обертовому моменті.
Формула умови рівноваги важеля
На малюнку нижче показаний типовий важіль, а також відзначені значення його правого і лівого плечей. Зовнішня сила позначена буквою F, а вага вантажу, який слід підняти, позначений буквою R.
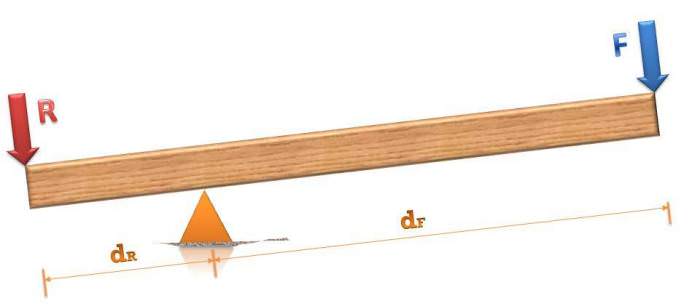
У статиці для того, щоб система базувалася, необхідно виконання двох умов:
Перше з названих умов означає відсутність поступального переміщення системи. Воно очевидно для важеля, оскільки його опора міцно стоїть на підлозі або землі. Тому перевірка умови рівноваги важеля передбачає лише перевірку справедливості наступного виразу:
∑i=1nMi = 0
Оскільки в нашому випадку діють тільки три сили, перепишемо цю формулу таким чином:
R*dR – F*dF + N*0 = 0
Сила реакції опори моменту не створює. Останній вираз перепишемо у вигляді:
R*dR = F*dF
Це і є умова рівноваги важеля (в 7 класі загальноосвітніх шкіл в курсі фізики воно вивчається). Формула показує: якщо значення сили F буде більше ваги вантажу R, то плече dF повинно бути менше плеча dR. Останнє означає, що, докладаючи велику силу протягом невеликого шляху, ми можемо перемістити вантаж на велику відстань. Справедлива і зворотна ситуація, коли F<R і, відповідно, dF>dR. У цьому випадку виграш спостерігається в силі.
Завдання зі слоном і мурахою
Багатьом відомий знаменитий вислів Архімеда про можливості з допомогою важеля зрушити цілу земну кулю. Це смілива заява має фізичний сенс, якщо врахувати формулу рівноваги важеля, записану вище. Залишимо Архімеда і Землю в спокої і вирішимо дещо іншу задачу, яка є не менш цікавою.
Слона і мурашки помістили на різні плечі важеля. Припустимо, що центр мас слона знаходиться в одному метрі від опори. На якій відстані від опори повинен знаходитися мураха, щоб врівноважити слона?
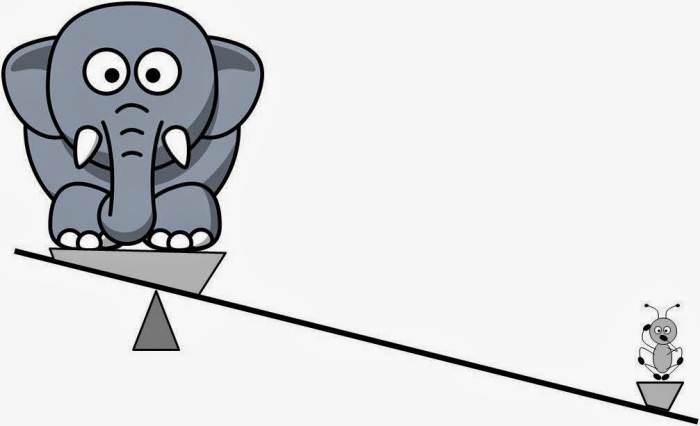
Щоб відповісти на запитання задачі, звернемося до табличними даними про масах розглянутих тварин. Масу мурашки візьмемо 5 мг (5*10-6 кг), масу слона будемо вважати рівною 5000 кг. Використовуючи формулу рівноваги важеля, отримуємо:
5000*1 = 5*10-6*x =>
x = 5000/(5*10-6) = 109 м.
Мураха може врівноважити слона, але для цього він повинен розташовуватися від опори важеля на відстані 1 мільйон кілометрів, що відповідає 1/150 відстані від Землі до Сонця!
Завдання з опорою на кінці балки
Як було зазначено вище, у важеля опора під балкою може розташовуватися в будь-якому місці. Припустимо, що вона знаходиться поблизу одного з кінців балки. Такий важіль має єдине плече, як показано нижче на малюнку.

Припустимо, що вантаж (червона стрілка) має масу 50 кг і розташований посередині плеча важеля. Якої величини повинна бути зовнішня сила F (синя стрілка), яка прикладена до кінця плеча, щоб врівноважити цей вантаж?
Позначимо довжину плеча важеля буквою d. Тоді можна записати умову рівноваги в наступному вигляді:
F*d = R*d/2 =>
F = m*g/2 = 50*9,81/2 = 245,25 Н
Таким чином, величина прикладеної сили повинна бути в два рази менше ваги вантажу.

Даний тип важеля використовується в таких винаходах, як ручна тачка для переміщення вантажів або орехокол.