Часто в задачах шкільного курсу геометрії доводиться вирішувати завдання, які вимагають використання комплексного підходу. Однією з таких завдань є обчислення об’єму піраміди за координатами вершин. Як вирішити цю геометричну задачу – відповість наведена нижче стаття.
Що являє собою піраміда?
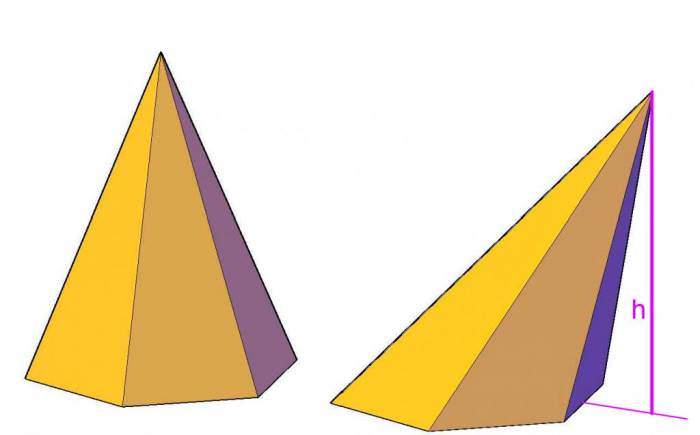
Кажучи простими словами, під цією фігурою розуміють просторовий об’єкт, обмежений трикутними сторонами і однієї багатокутної гранню, яка називається основою. Многоугольное основа може бути довільним n-кутником на площині, наприклад, правильним трикутником, паралелограмом і так далі.
Будь-яка піраміда має n + 1 грань, 2 * n ребер і n + 1 вершину. Вершини фігури не є рівноправними. Так, існує єдина вершина, яка не належить основи. Вона називається головною. Відстань від неї до площині підстави – це висота фігури.
Піраміди можуть бути похилими, якщо висота перетинає основу не в його центрі, або прямими, коли висота з підставою перетинається в геометричному центрі останнього. Також фігури можуть бути неправильними і правильними. Піраміди правильні складаються з рівнокутного і рівностороннього підстави і декількох рівнобедрених трикутників, які одне одному рівні.